в) Предположим, нам удалось вычеркнуть n сумм.
С одной стороны, сумма всех вычеркнутых чисел не меньше 1 + 2 + 3 + ... + 3n = 3n (3n + 1)/2; с другой стороны, сумма вычеркнутых чисел не больше 39 + 38 + 37 + ... + (40 - n) = n (79 - n) / 2. Поэтому n (79 - n) / 2 ≥ 3n (3n + 1)/2; 79 - n ≥ 9n + 3; n ≤ 7.
Покажем, что n = 7 возможно:
1 + 15 + 23 = 39
2 + 14 + 22 = 38
3 + 13 + 21 = 37
4 + 12 + 20 = 36
5 + 11 + 19 = 35
6 + 10 + 18 = 34
7 + 9 + 17 = 33
а) Например, первые 6 примеров выше
б) Нет, по доказанному
ответ. б) нет; в) 7
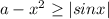
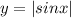расположен выше оси ОХ. 
.
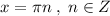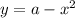- это параболы , ветви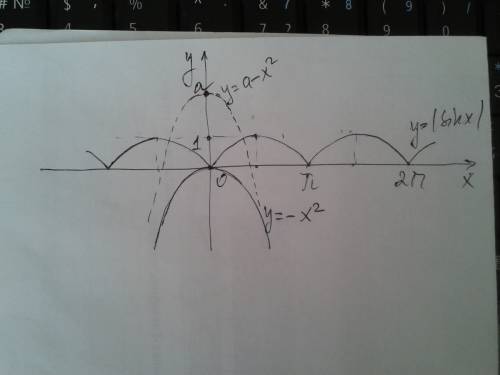
ПОСТАВЬ НА ОТВЕТ
Объяснение:
Давайте начнем решение уравнения 0.2x + 0.2x^2 * (8x - 3) = 0.4x^2 * (4x - 5) с выполнения открытия скобок в обеих частях его.
Применим для этого правило умножения одночлена на многочлен. Применим и получаем:
0.2x + 0.2x^2 * 8x - 0.2x^2 * 3 = 0.4x^2 * 4x - 0.4x^2 * 5;
0.2x + 1.6x^3 - 0.6x^2 = 1.6x^3 - 2x^2;
Переносим все слагаемые из правой части уравнения в левую и приведем подобные:
1.6x^3 - 1.6x^3 + 2x^2 - 0.6x^2 + 0.2x = 0;
1.4x^2 + 0.2x = 0;
0.2x(7x + 1) = 0;
1) 0.2x = 0;
x = 0;
2) 7x + 1 = 0;
7x = -1;
x = -1/7,
ответ: -1/7.