четвертое х€(2,3;∞)
Объяснение
Дано неравенство.Линейная функция (3-х) убывающая, а показательная (3^х) возрастающая для всех х€R.
При х=0 3>1-неравенство не выполняется, значит возможные решения лежат в интервалах 2 и 4.
При х=0.7 2.3>2.158 -неравенство не выполняется, значит х=0.7 и бесконечно близкие к нему значения не входят в область решений. Возьмем х=0.74, получим 2.26>2.255 -опять не выполняется, а при х=0.742 2.258<2.260 -выполняется. Значит нижней границей интервала значение х=0.7 не является, поскольку при значениях 0.7<х<0.74 (например) неравенство не выполняется.
На 4м интервале неравенство верное для всех х этого интервала, включая даже х=2.3
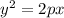ее фокус находится в точке с координатами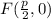 
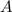находиться в системе уравнения 
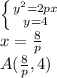Если уравнение касательной равна 
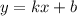с учетом того что она проходит через точку 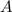получаем 
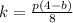, подставляя 
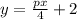
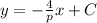он проходит через точку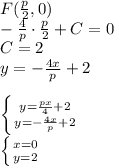 
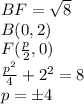
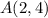
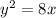
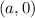центр окружности (так как центр лежит на оси 
) 
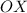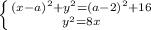
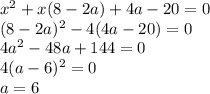
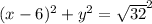
9. 2х-5=21х+28+5
2х-21х=28+5+5
-19х=38
х=38÷(-19)
х= -2
2×(-2)-5=7(3×(-2)+4)+5
-9= -9
10. 28-4(3х+2)=5(2х-7)
28-12х-8=10х-35
-12х-10х=8-35-28
- 22х=- 55
х= -55÷(-22)
х=2,5
28-4(3×2,5+2)=5(2×2,5-7)
-10=-10
11. 3х-4(5х+2)-6(3х-4)=1
3х-20х-8-18х+24=1
3х-20х-18х=1+8-24
-35х=-15
х=-15÷(-35)
х=- 15÷(-35)
х= -3/7
3×3/7-4(5×3/7+2)-6(3/7-4)=1
12. 7(х-4)+3=-5(2х-7)+х-8
7х-28+3= -10х+35+х-8
7х+10х-х=35-8+28-3
16х=52
х=52÷16
х=3,25