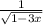
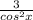
Объяснение:
\left\{\begin{matrix}x\in \begin{bmatrix}-\sqrt{-\left(y-5\right)\left(y+1\right)},\sqrt{-\left(y-5\right)\left(y+1\right)}\end{bmatrix}\text{, }&y\geq -1\text{ and }y\leq \frac{3-\sqrt{17}}{2}\\x=\sqrt{\left(5-y\right)\left(y+1\right)}\text{, }&y=\frac{\sqrt{17}+3}{2}\\x\in \begin{bmatrix}y-1,\sqrt{-\left(y-5\right)\left(y+1\right)}\end{bmatrix}\text{, }&y>\frac{3-\sqrt{17}}{2}\text{ and }
y<\frac{\sqrt{17}+3}{2}\end{matrix}\right.
\left\{\begin{matrix}y=2\text{, }&x\geq 1\text{ and }x\leq 3\\y\in \begin{bmatrix}-\sqrt{9-x^{2}}+2,\sqrt{9-x^{2}}+2\end{bmatrix}\text{, }&x\geq \frac{\sqrt{17}+1}{2}\text{ and }x<3\\y=x+1\text{, }&x=\frac{1-\sqrt{17}}{2}\\y\in \begin{bmatrix}-\sqrt{9-x^{2}}+2,x+1\end{bmatrix}\text{, }&\left(x>\frac{1-\sqrt{17}}{2}\text{ and }x<\frac{\sqrt{17}+1}{2}\text{ and }|x|<3\right)\text{ or }\left(x\geq 1\text{ and }x<\frac{\sqrt{17}+1}{2}\right)\end{matrix}\right.
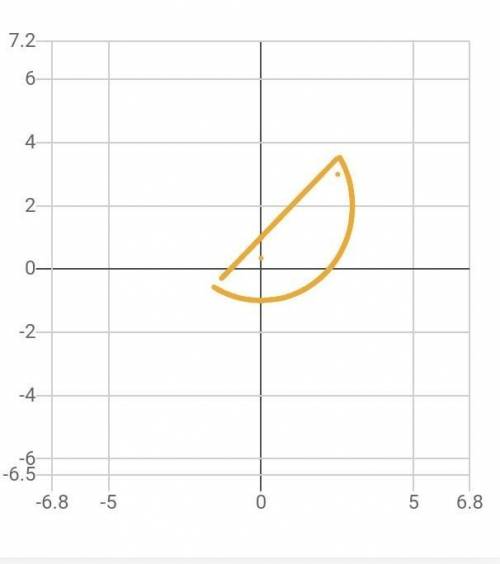
В решении.
Объяснение:
1)
а)√72 = √36*2 = 6√2;
б)0,01*√800 = 0,01*√100*8 = 0,01*10√8 = 0,1√8;
в)√28 = √4*7 = 2√7;
г)0,2√75 = 0,2*√25*3 = 0,2*5√3 = √3;
д)√98 = √49*2 = 7√2;
е)0,02*√1200 = 0,02*√400*3 = 0,02*20√3 = 0,4√3;
ж)1/5*√50 = 0,2*√25*2 = 0,2*5√2 = √2;
з)√27 = √9*3 = 3√3.
2)
а)3√5а = √9*5а = √45а;
б)-10√0,2b = -√100*0,2b = -√20b;
в)5√2а = √25*2а = √50а;
г)-20√0,1b = -√400*0,1b = -√40b;
д)4√5 = √16*5 = √80;
е)-3√а = -√9а;
ж)9√2 = √81*2 = √162;
з)2√b = √4b.
3)
а) √27 и 4√3
√27 = √9*3 = 3√3
√27 < 4√3;
б)√18 и 4√2
√18 = √9*2 = 3√2
√18 < 4√2
в)3√2 и 2√3
3√2 = √9*2 = √18; 2√3 = √4*3 = √12
3√2 > 2√3;
г)5√3 и 3√5
5√3 = √25*3 = √75; 3√5 = √9*5 = √45
5√3 > 3√5.