1.
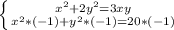
Сложим:
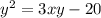
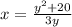
Подставим 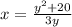во второе уравнение 
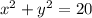и получим:
<=> 
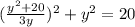
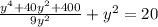
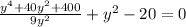
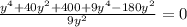
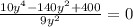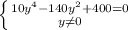
Замена:
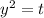
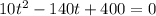
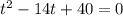
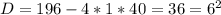
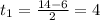
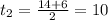
Замена:
=> 
=> 
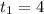
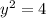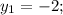
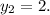
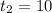
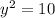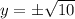
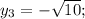
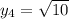
Находим значения переменной 
, подставляя значения 
в :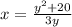
при:
=> 
=> 
=> 
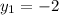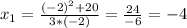
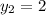
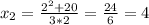
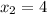
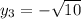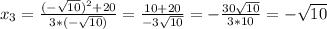
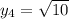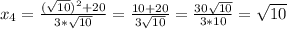
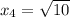
ответ: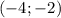 
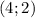
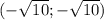
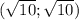
x=4-y²
2) 2-2y=4-y²
x=2-2y
3)y²-2y-2=0
x=2-2y
решим 1 уравнение у²-2у-2=0 D=2²-4*(-2)=12 y=2-√12/2=2-2√3)/2=2*(1-√2)/2=1-√3
y2=2+√12)/2=1+√3
4)y=1-√3 или н=1+√3
х=2-2*(1-√3)=2√3 х=2+2*(1+√3)=2+2+2√3=4+2√3
в)х²+у²=29
у=10/х
2) х²+(10/х)²-29=0
у=10/х решим 1 уравнение Приведем к общему знаменателю получим
х^4-29x²+10=0 пусть х²=n n²-29n+10=0 D=29²-4*1*10=841-40=801=9*89
n1=(29+√801)/2
что-то не так в условии то что написано верно точно