Рассмотрим два крайних случая, чтобы доказать, что количество ребят не зависит от распределения 16 юношей по двум классам. 1) Пусть все 16 юношей в классе А, а в классе Б юношей нет. Тогда девушек в 10 А столько же, сколько юношей в 10 Б, то есть 0. Значит, в классе А 16 юношей, а в классе Б 24 девушки. Всего 40 ребят.
2) Пусть все 16 юношей в классе Б, и там еще 24-16=8 девушек. В классе А юношей нет, а девушек столько же, сколько юношей в Б, то есть 16. Опять получается, что в классе А 16 ребят, а в Б 24, всего 40 ребят.
а)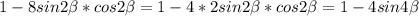
б)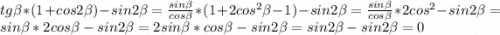
в)
г) ctg(45°-β)/1 - ctg²(45°-β) = ctg 45° × ctgβ +1/ctgβ - ctg 45° / 1 - (ctg 45° × ctgβ +1/ctgβ - ctg 45°)² = cotβ+1/ctgβ-1 / 1-(ctgβ+1/ctgβ-1)² = cotβ+1/ctgβ-1 / 1- (ctgβ+1)²/(ctgβ-1)² = cotβ+1/ctgβ-1 / (ctgβ-1)²-ctg(β+1)²/(ctgβ-1)² = cotβ+1/ctgβ-1 / -2×2ctgβ/(ctgβ-1)² = cotβ+1/ctgβ-1 / -4ctgβ/(ctgβ-1)² = - cotβ+1/ctgβ-1 / 4ctgβ/(ctgβ-1)² = - cotβ+1/ctgβ-1 × (ctgβ-1)²/4ctgβ = - (cotβ+1)×(ctgβ-1)/4ctgβ = - ctg²β-1/4ctgβ = 1-ctg²β/4ctgβ