составим систему
x^2+y^2=40
y=3x
поставим
x^2+9x^2=40
10x^2=40
x^2=4
x=+-2
первый случай, когда х=2 y=6 (2;6)
второй случай, когда х=-2 у=-6 (-2;-6)
Задание 1. - вложение 1
а) (x+9)(x-5)>0
f(x)=(x+9)(x-5)
Нули функции: -9; 5
ответ: (-∞; 9)∪(5; +∞)
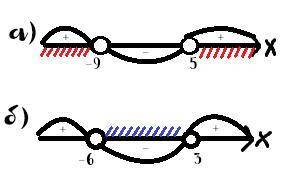
б)
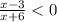
ОДЗ: x≠-6
(x-3)(x+6)<0
f(x)=(x-3)(x+6)
Нули функции: 3; -6
ответ: (-6; 3)
Задание 2.
а)
x³ - 49x = 0
x(x²-49)=0
x(x-7)(x+7)=0
x=0 или x=7 или x=-7
ответ: -7; 0; 7
б)
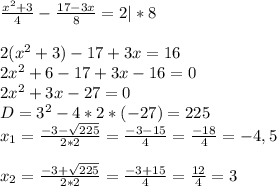
ответ: -4,5; 3
в) x⁴ - 17x² + 16 = 0
x² = t - новая переменная
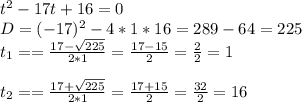
x² = 1 или x² = 16
x₁=-1 ; x₂=1 ; x₃=-4 ; x₄=4
ответ: ±1; ±4
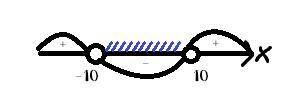
Задание 3. - вложение 2
D < 0, корней нет
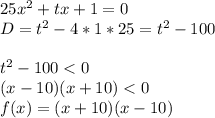
Нули функции: 10; -10
ответ: t∈(-10; 10)
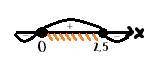
Задание 4. - вложение 3
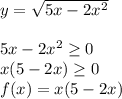
Нули функции: 0; 2,5
ответ: x∈[0; 2,5]
Это система.
X^2+y^2=40
y=3x
Подставим y
x^2+9x^2=40
10x^2=40
x^2=4
x=2
Теперь найдём y :
2^2+y^2=40
4+y^2=40
y^2=36
y=6