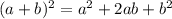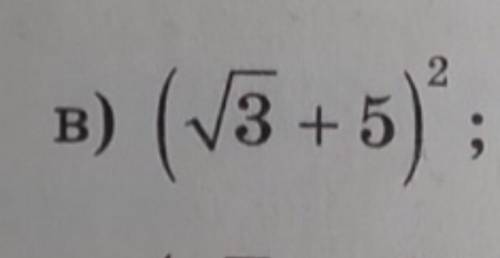
1) Т.к. это квадратичная функция, представленная параболой, найдем вершину параболы по следующей формуле:
Подставляем единичку в функцию:
2*1-4*1+1=2-4+1=2-3=-1.
Ниже график функции не будет подыматься, следовательно, множество значений:
y∈{-1...+∞}.
2)
Несмотря ни на что, под корнем НИКОГДА не должно быть отрицательное значение. Решаем 2 полноценных систем уравнения:
Но, -3<5 ⇒x≥5.
D(f)=x≥5
3) Вы, наверно, имели ввиду сумму корней.
Проведем замену переменной:
Решаем квадратное уравнение:
А теперь, решаем два уравнения:
Но, нежелательно в уравнение вставлять комплексные числа, т.е. второй вариант просто убираем. Получим единственный корень - √3.
Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде обыкновенной дроби {\displaystyle \pm {\frac {m}{n}}}{\displaystyle \pm {\frac {m}{n}}}, где {\displaystyle m,n}m,n — натуральные числа. Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.
Иррациональные числа
ζ(3) — ρ — √2 — √3 — √5 — ln 2 — φ,Φ — ψ — α,δ — e — {\displaystyle e^{\pi }}e^{\pi } и π
Другими словами, множество иррациональных чисел есть разность {\displaystyle \mathbb {I} =\mathbb {R} \backslash \mathbb {Q} }{\displaystyle \mathbb {I} =\mathbb {R} \backslash \mathbb {Q} } множеств вещественных и рациональных чисел.
О существовании иррациональных чисел (точнее отрезков, несоизмеримых с отрезком единичной длины), знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа {\displaystyle {\sqrt {2}}}{\sqrt {2}}[1].
К числу иррациональных чисел относятся отношение π окружности круга к его диаметру, число Эйлера e, золотое сечение φ и квадратный корень из двух[2][3][4]; на самом деле все квадратные корни натуральных чисел, кроме полных квадратов, иррациональны.
Иррациональные числа также могут рассматриваться через бесконечные непрерывные дроби. Следствием доказательства Кантора является то, что действительные числа неисчислимы, а рациональные счетны, отсюда следует, что почти все действительные числа иррациональны[5].
Объяснение:
по формуле