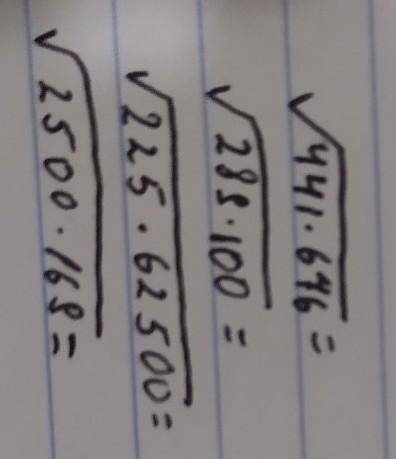
1. Преобразуем уравнение:
4х^2 + 12х + 12/х + 4/х^2 = 47;
4(х^2 + 2 + 1/x^2) - 8 + 12(х + 1/х) - 47 = 0;
4(х + 1/x)^2 + 12(х + 1/х) - 55 = 0.
2. Замена:
х + 1/x = t;
4t^2 + 12t - 55 = 0;
D/4 = 6^2 + 4 * 55 = 36 + 220 = 256 = 16^2;
t = (-6 ± 16)/4;
t1 = (-6 - 16)/4 = -22/4 = -11/2;
t2 = (-6 + 16)/4 = 10/4 = 5/2.
3. Обратная замена:
х + 1/x = t;
х^2 + 1 = tx;
х^2 - tx + 1 = 0;
1) t = -11/2;
х^2 + 11/2 * x + 1 = 0;
2х^2 + 11x + 2 = 0;
D = 11^2 - 4 * 2 * 2 = 121 - 16 = 105;
x1/2 = (-11 ± √105)/4;
2) t = 5/2;
х^2 - 5/2 * x + 1 = 0;
2х^2 - 5x + 2 = 0;
D = 5^2 - 4 * 2 * 2 = 25 - 16 = 9;
x = (5 ± √9)/4 = (5 ± 3)/4;
x3 = (5 - 3)/4 = 2/4 = 1/2;
x4 = (5 + 3)/4 = 8/4 = 2.
ответ: (-11 ± √105)/4; 1/2; 2.
а) x²-8x+15=0
Д=64-60=4
№1
х1=8-2/2=3
х2=8+2/2=5
б) 9x²+6x+1=0
Д= 81-24=57
х1=-6-V57/18
х2=-6+V57/18
(если что знак V - это корень)
в) 3x²-11x-4=0
Д= 9-176=-167
НЕ ИМЕЕТ РЕШЕНИЯ (т.к. дискриминант получился отрицательным)
г) -5x²=7-2x
-5x²+2х-7=0
Д=25+56=81
х1=-2-9/-10=1,1
х2=-2+9/-10=-0,7
№2
С системы уравнений
Длина-х, ширина-у, тогда 2(х+у)=62 2х+2у=62|2 х+у=31 у=31-х
ху=220 ху=220 ху=220
Теперь подставим во второе: х(31-х)=220
-х²+31x-220=0 (все это уравнение умножаем на -1)
x²-31x+220=0 (это получилось после того как мы умножили на -1)
D=961-4*220=121
x1=31+11/2=21
x2=31-11/2=10
Подставляем наш ответ в первое уравнение: у1=31-21=10
у2=31-10=21
ответ: длина-21; 10; высота-10; 21.
№3
я не знаю как решать, но думаю это число 2
Вычисляем квадратный корень : 21*26
2)170
Вычисляем квадратный корень : 17*10
3)3750
Вычисляем квадратный корень : 15*250
4)650
Вычисляем квадратный корень: 50*13
Вроде так