(-5; 1; 1)
Объяснение:
Найдём уравнение прямой, перпендикулярной данной плоскости и проходящей через точку A. Направляющим вектором данной прямой является вектор нормали плоскости, то есть вектор {3; 2; 2}. Составим каноническое уравнение прямой:
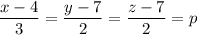
Из этого уравнения составим параметрическое уравнение:
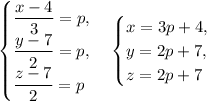
Чтобы найти точку пересечения прямой с плоскостью, то есть проекцию данной точки, подставим координаты из параметрического уравнения в уравнение плоскости:
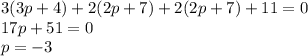
Подставляя найденное значение параметра, получим координаты искомой точки:
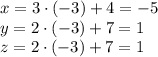
Значит , q = -5
B3 = B1 * q^2 = -6 * (-5)^2 = -150
B3 = -150