√f(x) ≥ g(x) ⇔ совокупности 2-х систем
1. f(x) ≥ 0
g(x) ≤ 0
2. g(x) > 0
f(x) ≥ g²(x)
√(10 - 7log(2) x + log²(2) x) ≥ 3 - log(2) x
одз x > 0 логарифм
(log(2) x - 2)(log(2) x - 5) > 0 корень
x ∈ (-∞,4] U [32, +∞)
общее x ∈ (0,4] U [32, +∞)
√((log(2) x - 2)(log(2) x - 5)) ≥ 3 - log(2) x
1. f(x) ≥ 0
g(x) ≤ 0
3 - log(2) x ≤ 0
(log(2) x - 2)(log(2) x - 5) ≥ 0
log(2) x = t
t ≥ 3
(t - 2)(t - 5) ≥ 0
[2] [5]
t ≤ 2
log(2) x ≤ 2
x ≤ 4
t ≥ 5
log(2) x ≥ 5
x ≥ 32
x ∈ [32, +∞)
2. g(x) > 0
f(x) ≥ g²(x)
3 - log(2) x > 0
x < 8
10 - 7log(2) x + log²(2) x ≥ (3 - log(2) x)²
10 - 7log(2) x + log²(2) x ≥ 9 - 6log(2) x + log²(2) x
1 ≥ log(2) x
x ≤ 2
учитывая одз
решение x ∈ (0,2] U [32, +∞)
не являются решением натуральные х ∈ (2, 32)
29 чисел от 3 до 31
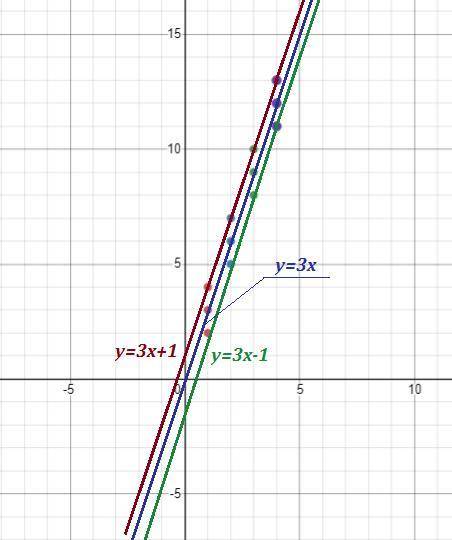
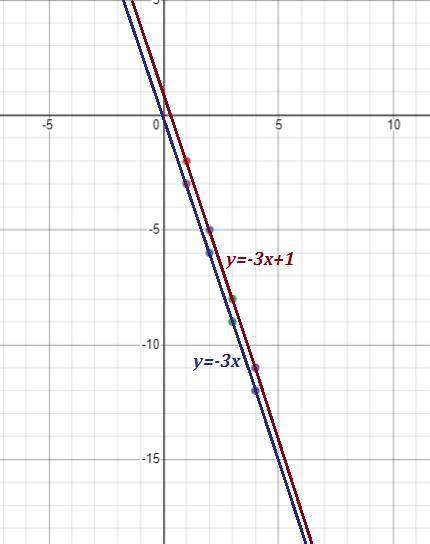
Чтобы с таблицы задать функцию, надо отметить точки на координатной плоскости и постараться увидеть закономерность. Все функции линейные, то есть графики - прямые линии .
1) у=3х , 2) у=3х+1 , 3) у=3х-1 , 4) у=-3х , 5) у=-3х+1 .
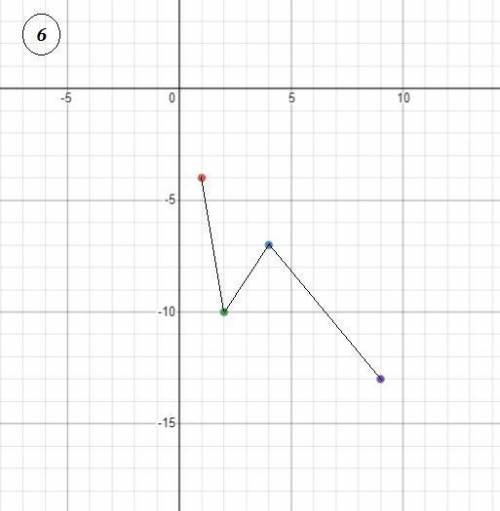
6) Здесь линейной закономерности не просматривается . Если бы в таблице значения "х" бы ли бы 1 , 2 , 3 , 4 , то есть таблица выглядела бы так
х | 1 | 2 | 3 | 4 |
y | -4 | -7 | -10 | -13 | , то функция имела бы вид у= -3х -1 .
В этом задании скорее всего была допущена описка .
x > 5
-___5___+
одз:
{2x - 4 > 0; x > 2
{x + 1 > 0; x > -1
ответ: (5; +бесконечности)