пояснения прилагаю.
1) 1.
⅓ =
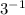
отсюда: - 1 × (x + 1) = - x - 1
2. так как основания одинаковы, можно от них "избавиться" и записать только показатели.
2) 1. выносим общий множитель за скобку, используя одно из свойств показательных выражений:
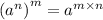
2. делим выражение на коэффициент при x
3. так как основания одинаковы, можно от них "избавиться" и записать только показатели.
3) 1. преобразовав выражение (от перемены мест множителей проивзедение не меняется),
можно сделать замену, приводящую уравнение к квадратному.
первый корень: x ∉ R, так как значения показательной функции всегда положительны (иными словами, если строить график, то ни x, ни y никогда не будут принимать отрицательные значения).

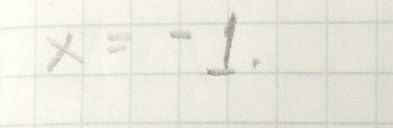
ответ: 4,2 м.
Объяснение:
1 комната длина в 1,5 раза больше ширины
2 комната -- длина --- 7,2 м.
общая площадь равна 56,7 м².
обозначим ширину через х м.
длина 1 комнаты --- 1,5х
Площадь 1 комнаты --- 1,5х²
Площадь второй комнаты --- 7,2х
1.5х²+7,2х=56,7;
1.5x²+7.2x-56.7=0;
a=1.5; b=7.2; c=-56.7.
D=b²-4ac=(7.2)²-4*1.5*(-56.7)=51.84+340.2=392.04 (19.8²)
x1=4.2; x2= - 9 - не соответствует условию задачи
Ширина комнат равна 4,2 м.
Проверим:
(1,5*4,2+7,2) * 4,2= 13,5*4,2=56, 7 м². Всё верно!
2. а(х^2-4)=а(х-2)(х+2)
3. 3(х^2-25а^2)=3(х-5а)(х+5а)
4. 2a(-y^2+a^2)=2a(a-y)(a+y)
5. 10ab+(5a^2-5b^2)=10ab+5(a-b)(a+b)
6. a(x^2-2xy+y^2)=a(x-y)^2
7. 12ab+(-6a^2-6b^2)=12ab-6(a^2-b^2)=12ab-6(a+b)(a-b)