Алгебра: Найди значение выражения : -5cos 154°/cos 26° • cos 120° - 20

Объяснение: Метод Гаусса.Запишем систему в виде расширенной матрицы:Добавим 2-ю строку к 1-й, предварительно умножив 2-ю строку на (-1):Добавим 3-ю строку ко 2-й, предварительно умножив 2-ю строку на 4, а 3-ю строку на (-1):Добавим 4-ю строку к 3-й, предварительно умножив 4-ю строку на (-2):Добавим 2-ю строку к 1-й, предварительно умножив 2-ю строку на 2:Добавим 3-ю строку ко 2-й, предварительно умножив 3-ю строку на (-1):Добавим 2-ю строку к 1-й, предварительно...

Найди значение выражения : -5cos 154°/cos 26° • cos 120° - 20

👇

Увидеть ответ

Ответ:

vbnioo

12.10.2022

решение в прикрепленном фото

Объяснение:

Найди значение выражения : -5cos 154°/cos 26° • cos 120° - 20

4,7(70 оценок)

Открыть все ответы

Ответ:

tanaletinaaaaa

12.10.2022

Преобразуем 2 уравнение:

(x+y)^2-(x+y)=0

(x+y)(x+y-1)=0 - произведение равно 0, если хотя бы один множитель равен 0

в 1 уравнении делаем замену:

xy=t

получим:

t^2+2t=3

t^2+2t-3=0

D=4+12=16=4^2

t1=(-2+4)/2=1

t2=(-2-4)/2=-3

система разделится на 4 системы

1) xy=1

x+y=0

x=-y

-y^2=1

y^2=-1

y - нет решений

2) xy=1

x+y-1=0

x=1-y

(1-y)y=1

-y^2+y-1=0

y^2-y+1=0

D<0

y - нет корней

3) xy=-3

x+y=0

x=-y

-y^2=-3

y^2=3

y1=sqrt(3)

y2=-sqrt(3)

x1=-sqrt(3)

x2=sqrt(3)

4) xy=-3

x+y-1=0

x=1-y

(1-y)*y=-3

-y^2+y=-3

-y^2+y+3=0

y^2-y-3=0

D=1+12=13

y3=(1+sqrt(13))/2

y4=(1-sqrt(13))/2

x3=1-(1+sqrt(13))/2=(2-1-sqrt(13))/2=(1-sqrt(13))/2

x4=1-(1-sqrt(13))/2=(2-1+sqrt(13))/2=(1+sqrt(13))/2

ответ: (-sqrt(3);sqrt(3)), (sqrt(3);-sqrt(3)), ((1-sqrt(13))/2;(1+sqrt(13))/2), ((1+sqrt(13))/2;(1-sqrt(13))/2)

Объяснение:

вродебы так

4,6(80 оценок)

Ответ:

DarckGh0st

12.10.2022

Объяснение:

$\left\{\begin{array}{}x_1+2x_2+3x_3+4x_4=7\\x_1+2x_3+2x_4=5\\4x_1+x_2-x_3=3\\2x_1+x_2+x_3=1\end{array}\right..$

Метод Гаусса.

Запишем систему в виде расширенной матрицы:

$\left(\begin{array}{}1&2&3&4&7\\1&0&2&2&5\\4&1&-1&0&3\\2&1&1&0&1\end{array}\right) .$

Добавим 2-ю строку к 1-й, предварительно умножив 2-ю строку

на (-1):

$\left(\begin{array}{}0&2&1&2&2\\1&0&2&2&5\\4&1&-1&0&3\\2&1&1&0&1\end{array}\right) .$

Добавим 3-ю строку ко 2-й, предварительно умножив 2-ю строку

на 4, а 3-ю строку на (-1):

$\left(\begin{array}{}0&2&1&2&2\\0&-1&9&8&17\\4&1&-1&0&3\\2&1&1&0&1\end{array}\right) .$

Добавим 4-ю строку к 3-й, предварительно умножив 4-ю строку

на (-2):

$\left(\begin{array}{}0&2&1&2&2\\0&-1&9&8&17\\0&-1&-3&0&1\\2&1&1&0&1\end{array}\right) .$

Добавим 2-ю строку к 1-й, предварительно умножив 2-ю строку

на 2:

$\left(\begin{array}{}0&0&19&18&36\\0&-1&9&8&17\\0&-1&-3&0&1\\2&1&1&0&1\end{array}\right) .$

Добавим 3-ю строку ко 2-й, предварительно умножив 3-ю строку

на (-1):

$\left(\begin{array}{}0&0&19&18&36\\0&0&12&8&16\\0&-1&-3&0&1\\2&1&1&0&1\end{array}\right) .$

Добавим 2-ю строку к 1-й, предварительно умножив 1-ю строку

на 12, а 2-ю строку на (-19):

$\left(\begin{array}{}0&0&0&64&128\\0&0&12&8&16\\0&-1&-3&0&1\\2&1&1&0&1\end{array}\right) .\ \ \ \ \Rightarrow$

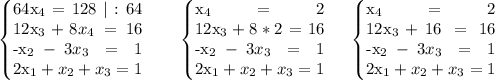
$\left\{\begin{array}{}64x_4=128\ |:64\\12x_3+8x_4=16\\-x_2-3x_3=1\\2x_1+x_2+x_3=1\end{array}\right.\ \ \ \ \ \ \left\{\begin{array}{}x_4=2\\ 12x_3+8*2=16\\-x_2-3x_3=1\\2x_1+x_2+x_3=1\end{array}\right.\ \ \ \ \left\{\begin{array}{}x_4=2\\ 12x_3+16=16\\-x_2-3x_3=1\\2x_1+x_2+x_3=1\end{array}\right.\\$

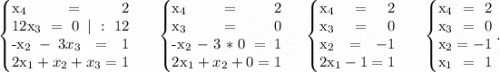
$\left\{\begin{array}{}x_4=2\\ 12x_3=0\ |:12\\-x_2-3x_3=1\\2x_1+x_2+x_3=1\end{array}\right.\ \ \ \ \ \left\{\begin{array}{}x_4=2\\ x_3=0\\-x_2-3*0=1\\2x_1+x_2+0=1\end{array}\right.\ \ \ \ \left\{\begin{array}{}x_4=2\\ x_3=0\\x_2=-1\\2x_1-1=1\end{array}\right.\ \ \ \ \ \left\{\begin{array}{}x_4=2\\ x_3=0\\x_2=-1\\x_1=1\end{array}\right..$