2x-3/x^2+1<= 0
Пусть 2x-3/x^2+1= 0, тогда
2x-3/x^2+1= 0
3x^2-2x-1=0
D=4+12=16
Корень из D=4
x1,2=(2+-4)/6
x1=1 и x2=-1/3
Ну и пишешь в системе(в скобках), что x<=1 и x<=-1/3
Строишь рисунок и получается:
(-&;-1/3] (&-это знак бесконечности)
Объяснение:
Сначала решим уравнение четвертой степени.
По теореме Безу его корни надо искать среди делителей свободного члена (в нашем случае свободный член равен 24)
Простым подбором, получаем 2 корня:
x = -2 и x= -3
Далее найдем произведение:
(x+2)·(x+3) = x² + 5x + 6
Разделим исходное уравнение на полученное произведение "столбиком"
Итак, неравенство можно написать так:
(x+2)(x+3)(x²+4) > 0
Поскольку (x²+4)>0, то по правилу интервалов находим решение неравенства:
(x+2)(x+3)>0
Получили:
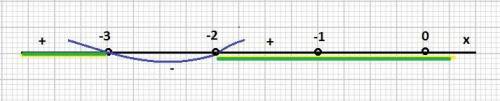
x ∈ (-∞; - 3) ∪ (-2; +∞)

-3x^2+2x+1=0
D=b^2-4ac
D= 2^2-4*(-3)*1
D= 16
x1= -b+ корень из D/2a
x1= (-2+4)/2*(-3)
x1=1/3
x2= -b- корень из D/2a
x2= (-2-4)/2*(-3)
x2=1