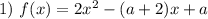 — квадратичная функция, график которой — парабола с ветвями, направленными вверх.
— квадратичная функция, график которой — парабола с ветвями, направленными вверх.
Нули функции:
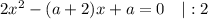
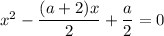
Согласно теореме Виета, имеем:
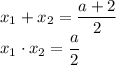
По условию 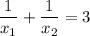 или
или 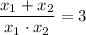 .
.
Следовательно, подставляя значения 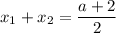 и
и 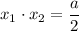 , найдем параметр
, найдем параметр  :
:
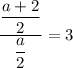
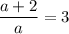
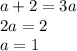
Таким образом, 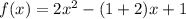 , то есть
, то есть 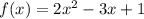
Найдем координаты точки вершины параболы:
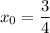
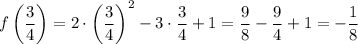
Значит, 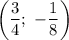 — точка вершины параболы.
— точка вершины параболы.
Найдем точки пересечения с осями координат:
а) С осью абсцисс:
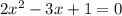
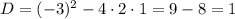
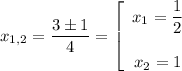
Следовательно, 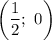 и
и 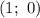 — точки пересечения функции с осью абсцисс.
— точки пересечения функции с осью абсцисс.
б) С осью ординат:
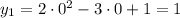
Следовательно, 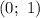 — точка пересечения с осью ординат.
— точка пересечения с осью ординат.
Согласно свойству симметрии параболы, 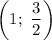 — точка графика.
— точка графика.
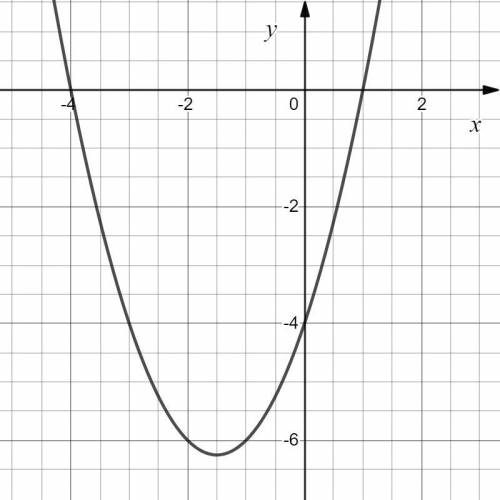
Изобразим график данной функции (см. вложение).
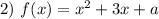 — квадратичная функция, график которой — парабола с ветвями, направленными вверх.
— квадратичная функция, график которой — парабола с ветвями, направленными вверх.
Нули функции:
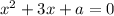
Согласно теореме Виета, имеем:
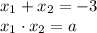
По условию 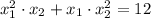
Следовательно, подставляя значения 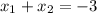 и
и 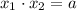 , найдем параметр
, найдем параметр  :
:
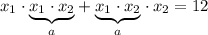
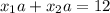
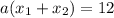
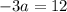
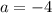
Таким образом, 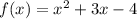
Найдем координаты точки вершины параболы:
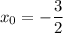
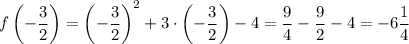
Найдем точки пересечения с осями координат:
а) С осью абсцисс:
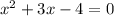
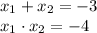
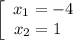
Следовательно, 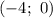 и
и 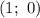 — точки пересечения функции с осью абсцисс.
— точки пересечения функции с осью абсцисс.
б) С осью ординат:
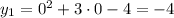
Следовательно, 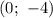 — точка пересечения с осью ординат.
— точка пересечения с осью ординат.
Согласно свойству симметрии параболы, 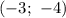 — точка графика.
— точка графика.
Изобразим график данной функции (см. вложение).
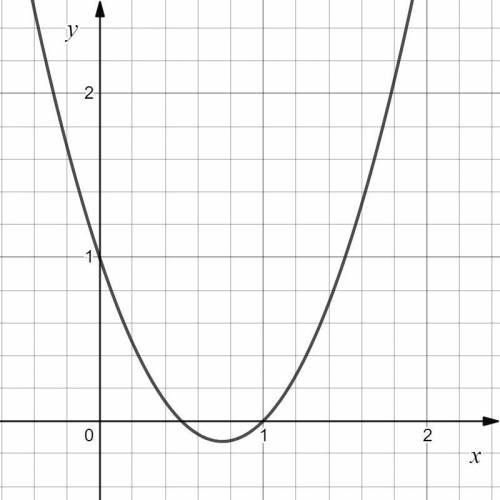
Знаю не все , но только это могу . Не уверенна на 100 процентов , что хоть это правильно.