(см. объяснение)
Объяснение:
Введем функции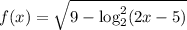 
и 
. Про вторую сразу скажем, что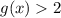 
, но на этом не остановимся. Видим, что в степени у нас модуль, а значит самое маленькое, что мы можем получить - это 
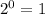при 
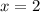или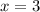 
. Тогда наименьшее значение этой функции будет равно 
.
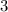Теперь разберемся с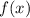 
. У нас есть квадратный корень, поэтому все значения функции точно 
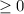. Но и здесь мы идем дальше. Поменяем временно 
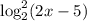на букву 
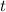. Тогда будет 
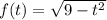. Под корнем парабола, ветви которой направлены вниз, а значит есть наибольшее значение, равное 
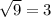при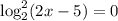 
, откуда .
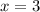Наибольшее значение 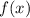равно 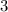и достигается при 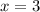. Наименьшее значение 
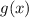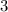равно и достигается пр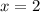и или .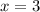
Тогда единственный корень исходного уравнения .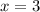
Уравнение решено!
3(8x-4x²+2x²-x³) < 0
24x-12x²+6x²-3x³ < 0 | :(-3)
-8x+4x²-2x²+x³ < 0
x³+2x²-8x < 0
x(x²+2x-8) < 0
Найдем нули функции:
y = 0
y = x(x²+2x-8)
⇒ x = 0 или x²+2x-8 = 0
D = 4+32 = 36
x₁ =
x₂ =
_______ ______ ______ ___________
-- \ / + \ / -- \ / +
----------- °----------- °------------°-------------------->
//////////// -4 0 /////////// 1,5 х
ответ: х ∈ (-∞ ; -4) U (0 ; 1,5)