Влыжных гонках участвуют 13 спортсменов из россии, 2 спортсмена из норвегии и 5 спортсменов из швеции. порядок, в котором спортсмены стартуют, определяется жребием. найдите вероятность того, что первым будет стартовать спортсмен не из россии.

👇

Увидеть ответ

Ответ:

martynenko5

11.10.2021

1+2+5=20

2+5=7

7/20=0,35

4,7(89 оценок)

Ответ:

marinavn2008

11.10.2021

13+2+5=20 Всего спортсменов
Не из России спортсменов 2+5=7
Узнаем вероятность
7:20=0.35

4,4(81 оценок)

Открыть все ответы

Ответ:

Dima140916

11.10.2021

Попробую. Тут недавно был аналогичный вопрос.
$ln(3x-1)* \sqrt{x^2-8x+8a-a^2} =0$
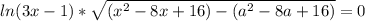
$ln(3x-1)* \sqrt{(x^2-8x+16)-(a^2-8a+16)} =0$
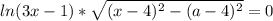
$ln(3x-1)* \sqrt{(x-4)^2-(a-4)^2} =0$
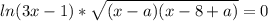
$ln(3x-1)* \sqrt{(x-a)(x-8+a)} =0$
Корни этого уравнения:
1) ln(3x - 1) = 0; 3x - 1 = 1; x1 = 2/3 ∈ [0; 4]
2) x2 = a
3) x3 = 8 - a
Нам нужно, чтобы только 1 корень принадлежал [0; 4]
Это возможно в таких случаях:
1) x = 2/3 ∈ [0; 4], тогда (2/3 - a)(2/3 - 8 + a) >= 0
-(a - 2/3)(a - 22/3) >= 0
a ∈ [2/3; 22/3]

2) x = a ∈ [0; 4], тогда
{ a ∈ [0; 4]
{ 3a - 1 > 0
Получаем
{ a ∈ [0; 4]
{ a > 1/3
a ∈ (1/3; 4]

3) x = 8 - a ∈ [0; 4]; тогда
{ a ∈ [4; 8]
{ 3(8 - a) - 1 > 0
Получаем
{ a ∈ [4; 8]
{ 24 - 3a - 1 > 0; a < 23/3
a ∈ [4; 23/3)
1 корень на интервале [0; 4] будет при a ∈ (1/3; 2/3] U [22/3; 23/3)
Это в случае, если все три корня x1 = 2/3; x2 = a; x3 = 8 - a различны.
Если же два корня совпадают, то могут быть варианты:
1) x1=x2=a=2/3 ∈ [0; 4], тогда x3=8-a=8-2/3=22/3 ∉ [0; 4] - 1 корень на [0; 4].
2) x1=x3=8-a=2/3 ∈ [0; 4], тогда x2=a=8-2/3=22/3 ∉ [0; 4] - 1 корень на [0; 4].
3) x2=x3=a=8-a, тогда x2=a=4 ∈ [0; 4] и x1=2/3 ∈ [0;4] - 2 корня на [0; 4].
ответ: a ∈ (1/3; 2/3] U [22/3; 23/3)

4,5(37 оценок)

Ответ:

Chinchil1a

11.10.2021

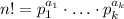Выведем общую формулу для разложения числа n! на простые множители. Запишем это разложение в виде $n!=p_1^{a_1}\cdot\ldots\cdot p_k^{a_k}$ , где p_i

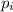- все простые числа не превосходящие n и a_i

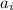- степени, с которыми они входят в это разложение, i=1,...,k. Докажем, что $a_i=[n/p_i]+[n/p_i^2]+[n/p_i^3]+\ldots$ , где [...] обозначает целую часть числа, т.е. для действительного числа х, запись [x] обозначает максимальное целое число не превосходящее х. Заметим, что в этой сумме всегда конечное число слагаемых, т.к. рано или поздно степень простого станет больше n, и с этого момента под целой частью будут числа меньшие 1, т.е. целая часть от них будет равна 0.

Доказательство. Пусть p - любое простое от 1 до n включительно. Понятно, что в разложении числа n! на простые множители будут встречаться только такие простые числа. Среди чисел 1, 2,...,n количество чисел делящихся на p равно [n/p]. Т.к. среди них есть числа делящиеся на p², p³,..., то количество чисел среди них, которые делятся на p только в первой степени равно [n/p]-[n/p²], т.е. мы из всех делящихся на р вычли все, делящиеся на р². Аналогично, количество чисел в ряду 1,...,n делящихся ровно на p² и не делящихся на p в степенях больших 2, равно [n/p²]-[n/p³]. Для степени p³ таких чисел будет [n/p³]-[n/p⁴] и т.д... Таким образом, количество чисел, у которых в разложении на простые p входит в разложение ровно в j-ой степени равно $[n/p^j]-[n/p^{j+1}]$ .

Значит в разложении n! на простые множители простое p входит в степени
([n/p]-[n/p²])+2([n/p²]-[n/p³])+3([n/p³]-[n/p⁴])+...=[n/p]+[n/p²]+[n/p³])+...
Как уже упоминал раньше, с некоторой степени все целые части [n/p^j]

будут равны 0, т.к. n/p^j

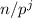станет меньше 1 при больших j (а именно, при j>[ln(n)/ln(p)]).

Итак, чтобы разложить число 1980! нужно подставить n=1980 в эту формулу. Получаем, что 2 входит в разложение в степени
[1980/2]+[1980/2²]+[1980/2³]+...+[1980/2¹⁰]=
=990+495+247+123+61+30+15+7+3+1=1972. Т.к. 1980/2¹¹<1, 1980/2¹²<1 и т.д., то все слагаемые после [1980/2¹⁰] будут равны 0.
Аналогично, [1980/3]+[1980/3²]+[1980/3³]+...+[1980/3⁶]=
=660+220+73+24+8+2=987. И т.д.
В итоге получаем то, что изображено на картинке.
Как разложить факториал число 1980! на простые множители?