Объяснение:
1 . ( x² - x )/3 = ( 2x + 4 )/5 ; │X 15 2 . ( 2x² + x )/5 = ( 4x - 2 )/3 ;│X 15
5( x² - x ) = 3( 2x + 4 ) ; 3( 2x² + x ) = 5( 4x - 2 ) ;
5x² - 5x = 6x + 12 ; 6x² + 3x = 20x - 10 ;
5x² - 5x - 6x - 12 = 0 ; 6x² + 3x - 20x + 10 = 0 ;
5x² - 11x - 12 = 0 ; 6x² - 17x + 10 = 0 ;
D = 361 > 0 ; x₁ = - 0,8 ; x₂ = 3 . D = 49 > 0 ; x₁ = 5/6 ; x₂ = 12/13 .
3 . ( x² - x )/2 = 5 + 6x ;│X 2
x² - x = 10 + 12x ;
x² - x - 12x - 10 = 0 ;
x² - 13x - 10 = 0 ; D = 209 > 0 ; x₁= (13 - √209 )/2 ; x₂ = (13 - √209 )/2 .


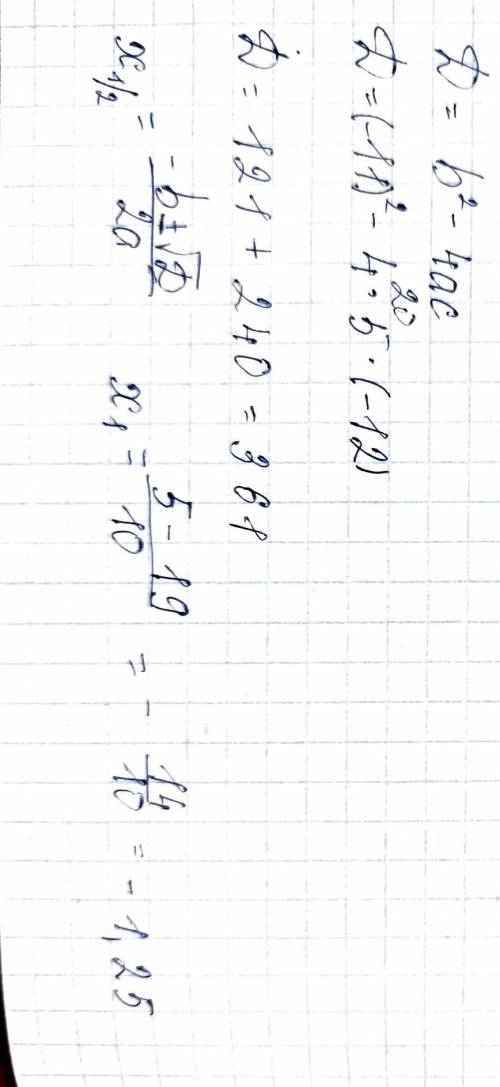
Очевидно, что такой случай возможен, если большее основание равно 2, а все остальные стороны равны по 1 (другово невозможно).(см.рисунок)
Если меньшее основание будет равно 2, то оно станет большим, и трапеция будет, такаяже, только перевернутой.
И так, так как у равнобокой трапеции, углы при основании равны, а так как меньшее основание, равно боковым сторонам, то все углы равно.
Сумма углов трапеции равна 180(градусов). Значит.
(угол) A= (угол) В= (угол) С= (угол)D=180/4=60.
Но так как, нас просили найти сумму углов при основании то,
ответ: сумма углов равна 60+60=120 (градусов)
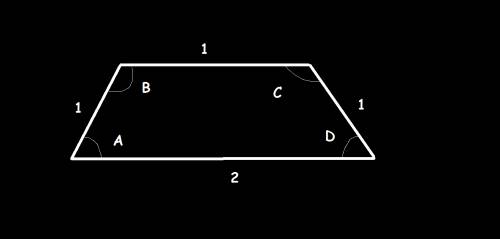
2. а^2-аb=a(a-b)
3. n(7-m)+k(7-m)=(n+k)(7-m)
4. 8m^2n-4mn^3=4mn(2m-n^2)
5. a(b-c)+3(b-c)=(a+3)(b-c)
6. 6a+9x=3(2a+3x)
7. ay-ax=a(y-x)
8. a^2-a^3b=a(a-a^2b)
9. 9n+6m=3(3n+2m)
10. b^2-ab=b(b-a)
11. b(a+5)-c(a+5)=(b-c)(a+5)
12. 20x^3y^2+4x^2y^3=4x^2y^2(5x+y)
13.6(n-m)+s(n-m)=(6+s)(n-m)
14. 16mn-4mn^3=4mn(4-n^2)
15.12(a+b)-x(a+b)=(12-x)(a+b)