Решение текстовых задач с составления уравнений и неравенств. Урок 2 Путешественник спустился на плоту вниз по течению реки за 24 ч, а обратно вернулся теплоходом за 3 ч. Найди собственную скорость теплохода, если скорость течения реки равна 4 км/ч. ответ: v =__км/ч.

👇

Увидеть ответ

Ответ:

Milka20060711

27.03.2022

ответ: 36 км/час.

Объяснение:

Решение.

Пусть собственная скорость теплохода равна х км/час.

Тогда скорость против течения равна х-4 км/час.

Расстояние, которое плот за 24 часа равно:

S=vt = 4*24 = 96 км.

Это расстояние путешественник на теплоходе за 3 часа

S=vt; 96=(x-4)*3;

3x-12=96;

3x=96+12;

3x= 108;

x= 36 км/час - собственная скорость теплохода.

Проверим:

S= 3*(36-4)= 3*32= 96 км. Всё верно!

4,5(79 оценок)

Открыть все ответы

Ответ:

BTS111111y

27.03.2022

Павел Петрович, Александр Павлович, Николай Павлович, Александр Николаевич, Александр Александрович, Николай Александрович.

Объяснение:

В списке нет царя по имени Петр, следовательно, Павел Петрович был первый из этих царей.

Других Павлов нет, следовательно, братья Александр Павлович и Николай Павлович правили сразу после Павла Петровича, сменив на троне один другого.

Таким образом, последний царь был Николай Александрович (других Николаев нет).

Александр Николаевич не мог править после последнего царя,

значит, он унаследовал трон после Николая Павловича, который,

следовательно, правил после своего брата Александра Павловича.

Тогда наследником Александра Николаевича и отцом Николая Александровича мог быть только

Александр Александрович.

4,4(2 оценок)

Ответ:

Xzxzxzxzxzzxzxz

27.03.2022

Уравнение четвёртой степени имеет вид:
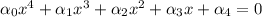
$\alpha _0x^4+ \alpha _1x^3+ \alpha _2x^2+ \alpha _3x+ \alpha _4=0$
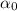Разделим обе части на коэффициент $\alpha _0$ , получаем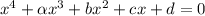
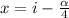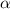$x^4+ \alpha x^3+ bx^2+cx+d=0$
где a, b, c, d – произвольные вещественные числа.

Уравнения вида приводится уравнение четвёртой степени, у которых отсувствует третьей степени., поэтому нужно сделать замену переменных, тоесть
$x=i- \frac{ \alpha }{4}$ , где $\alpha$ - коэффициент перед х^3 и 4 - произвольные вещественные числа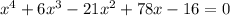

В нашем случае такое уравнение: x^4+6x^3-21x^2+78x-16=0

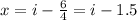Заменим $x=i- \frac{6}{4} =i-1.5$ , получаем
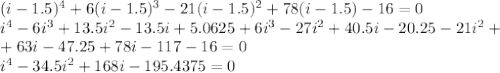
$(i-1.5)^4+6(i-1.5)^3-21(i-1.5)^2+78(i-1.5)-16=0\\ i^4-6i^3+13.5i^2-13.5i+5.0625+6i^3-27i^2+40.5i-20.25-21i^2+\\+63i-47.25+78i-117-16=0\\ i^4-34.5i^2+168i-195.4375=0$

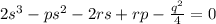
Получаем кубическое уравнение: $2s^3-ps^2-2rs+rp- \frac{q^2}{4}=0$
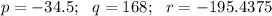
В нашем случае: $p=-34.5;\,\,\,\,q=168;\,\,\,\,r=-195.4375$
Подставляем и получаем уравнение
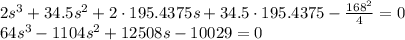
$2s^3+34.5s^2+2\cdot195.4375s+34.5\cdot195.4375- \frac{168^2}{4}=0\\ 64s^3-1104s^2+12508s-10029=0$
Разложим одночлены в сумму нескольких
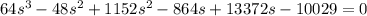
64s^3-48s^2+1152s^2-864s+13372s-10029=0

Выносим общий множитель
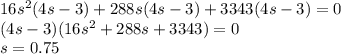
$16s^2(4s-3)+288s(4s-3)+3343(4s-3)=0\\ (4s-3)(16s^2+288s+3343)=0\\ s=0.75$
Уравнение 16s²+288s+3343=0 решений не имеет, так как D<0

Таким образом для решения уравнения остается квадратное уравнение
$i^2+i \sqrt{2s-p} - \frac{q}{2\sqrt{2s-p}}+s=0$
Заменяем
$i^2+i\sqrt{2\cdot0.75+34.5}- \frac{168}{\sqrt{2\cdot0.75+34.5}} +0.75=0\\ 4i^2+24i-53=0\\ D=b^2-4ac=576+848=1424\\ i= \dfrac{-6\pm \sqrt{89} }{2}$

Возвращаемся к замене
$x=i-1.5=\dfrac{-6\pm \sqrt{89} }{2}- \dfrac{3}{2} =\dfrac{-9\pm \sqrt{89} }{2}$

Окончательный ответ: $\dfrac{-9\pm \sqrt{89} }{2}.$