
1) х вершины = -b / 2a; х = 2 / -2 = -1.
у вершины = -1 + 2 + 3 = 4.
--------------------------------------
Хв = -1
Ув = 4
2) Ось симметрии параболы проходит через вершину. С этого график оси симметрии: x = -1.
--------------------------------------
х = -1
3) Точки пересечения с осью Х - корни квадратного уравнения. С этого они ровни:
-x^2 - 2x + 3 = 0,
x^2 + 2x - 3 = 0.
За теоремой Виета: x1 = -3; x2 = 1.
Точки пересечения с осью У узнаю подставляя вместо х 0.
0 - 0 + 3 = 3.
--------------------------------------
( 0, 3 ), ( -3, 0 ), ( 1, 0 )
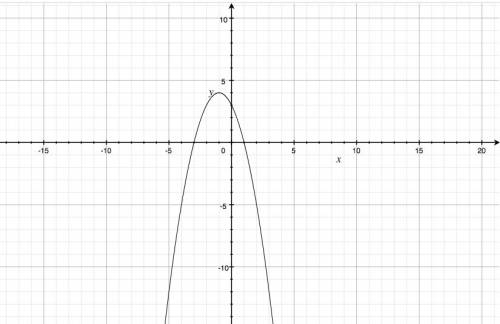
4) График в фото
5) -x^2 - 2x + 3 > 0;
Используя график видим, что функция больше 0 при х є ( -3 ; 1 ).
--------------------------------------
х є ( -3 ; 1 )
Объяснение: Точки функції є критичними, якщо похідна в цих точках =0. Критичні точки є точками max, коли похідна в цій точці змінює знак з + на -.
1) f'(x)=-2x+12, -2x+12=0, x=6
f'(5)=-2·5+12=2 +
f'(7)=-2·7+12=-2 -
Точка з абсцисою x=6 є точкою max
2)f'(x)=-4x³+16x, -4x³+16x=0, 4x·(4-x²)=0, 4x·(2-x)·(2+x)=0
x₁=0, x₂=2, x₃=-2 - критичні точки
f'(-3)=-4·(-3)³+16·(-3)=108-48=60 +
f'(-1)=-4·(-1)³+16·(-1)=4-16=-12 -
f'(1)=-4·1³+16·1=-4+16=12 +
f'(3)=-4·3³+16·3=-108+48=-60 -
Точки з абсцисами x₃=-2 і x₂=2 є точками max
3) f'(x)=6x²-6x, 6x²-6x=0, 6x(x-1)=0
x₁=0, x₂=1 критичні точки.
f'(-1)=6·(-1)²-6·(-1)=6+6=12 +
f'(1/2)=6·(1/2)²-6·(1/2)=3/2-3=-3/2 -
f'(5)=6·5²-6·5=150-30=120 +
Точка з абсцисою x₁=0 є точкою max
4) f'(x)= 2x³-2x, 2x³-2x=0, 2x(x²-1)=0, 2x(x-1)(x+1)=0
x₁=0, x₂=1, x₃=-1 - критичні точки
f'(-4)=2·(-4)³-2·(-4)=-128+8=-120 -
f'(-1/2)=2·(-1/2)³-2·(-1/2)=-1/4+1=3/4 +
f'(1/2)=2·(1/2)³-2·(1/2)=1/4-1=-3/4 -
f'(2)=2·2³-2·2=16-4=12 +
Точка з абсцисою x₁=0 є точкою max
100²
Объяснение:
109²=100×100=10000