В решении.
Объяснение:
1.
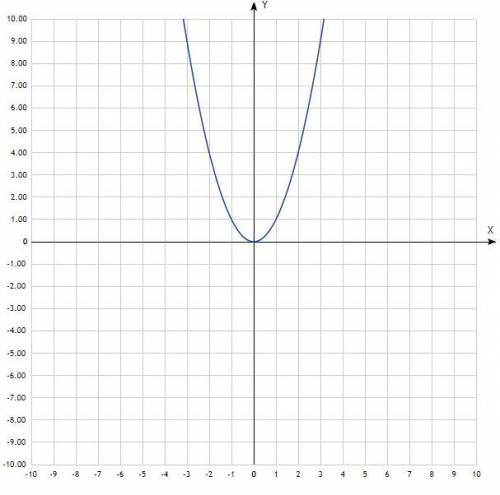
Постройте график функции у = х². Найдите наибольшее и наименьшее значение на отрезке [-1; 4].
Квадратичная функция, график - классическая парабола с вершиной в начале координат, ветви направлены вверх.
Придать значения х, подставить в уравнение, вычислить значения у, записать в таблицу.
Таблица:
х -4 -3 -2 -1 0 1 2 3 4
у 16 9 4 1 0 1 4 9 16
На отрезке [-1; 4] у наим. = 0; у наиб. = 16.
2. Упростите:
(4ас³в)² : (-2с²в)³ =
= 16а²с⁶в²/4с⁶в³ =
= 16/4(а²с⁶⁻⁶в²⁻³) =
= 4а²/в.
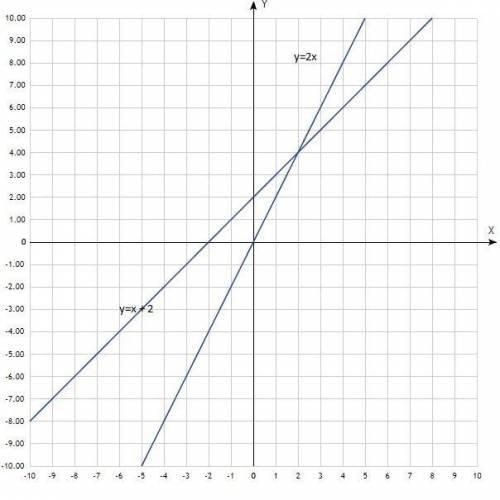
3. Решите систему уравнений графически.
у = 2х
у = х + 2
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
у = 2х у = х + 2
Таблицы:
х -1 0 1 х -1 0 1
у -2 0 2 у 1 2 3
Согласно графика, координаты точки пересечения прямых (2; 4).
Решение системы уравнений (2; 4).
ответ:Нам нужно разложить на множители выражение ac - ad - 5bc + 5bd для этого сгруппируем попарно первое со вторым и третье с четвертым слагаемые и вынесем общий множитель за скобки.
ac - ad - 5bc + 5bd = (ac - ad) - (5bc - 5bd);
Из первой скобки вынесем a, а из второй 5b, получим:
(ac - ad) - (5bc - 5bd) = a(c - d) - 5b(c - d).
Рассмотрим полученное выражение. В результате мы получили разность двух выражений каждое из которых содержит скобку (c - d), вынесем ее как общий множитель.
a(c - d) - 5b(c - d) = (с - d)(a - 5b).
ответ: (с - d)(a - 5b).
Объяснение: