Найти пропущенный трехчлен так, чтобы уравнение удовлетворялось. $1) {(x + y)}^{3} = (x + y)(...) \\ 2) {(x - y)}^{3} = (x - y)(...)$

👇

Ответ:

alex2007serg

08.06.2023

) чтобы получить x^3 нужно умножить x на x^2, аналогично с y^3, пусть трехчлен будет x^2+y^2. Раскрываем скобки: (x+y)(x^2+y^2) = x^3+y^3+x^2y+xy^2. Нужно избавиться от x^2y+xy^2 = xy(x+y), получается добавить -xy. ответ: x^2+y^2-xy.

2) Очевидно (x+y)^2

3) рассуждая как в 1), пробуем x^2+y^2, раскрываем скобки (x-y)(x^2+y^2) = x^3-y^3+xy^2-x^2y. Нужно избавиться от xy^2-x^2y = xy(y-x). ответ: x^2+y^2+xy.

4) Очевидно (x-y)^2

4,7(62 оценок)

Открыть все ответы

Ответ:

SKoteickaЗ

08.06.2023

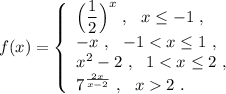
$f(x)=\left\{\begin{array}{l}\Big(\dfrac{1}{2}\Big)^{x}\ ,\ \ x\leq -1\ ,\\-x\ ,\ \ -1$

Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х= -1, х=1 , х=2 .

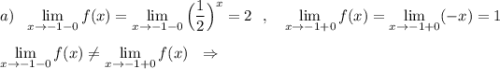
$a)\ \ \lim\limits _{x \to -1-0}f(x)=\lim\limits _{x \to -1-0}\Big(\dfrac{1}{2}\Big)^{x}=2\ \ ,\ \ \ \lim\limits _{x \to -1+0}f(x)=\lim\limits _{x \to -1+0}(-x)=1\\\\\lim\limits _{x \to -1-0}f(x)\ne \lim\limits _{x \to -1+0}f(x)\ \ \Rightarrow$

При х= -1 функция имеет разрыв 1 рода .

$b)\ \ \lim\limits _{x \to 1-0}f(x)=\lim\limits _{x \to 1-0}(-x)=-1\ ,\ \ \lim\limits _{x \to 1+0}f(x)=\lim\limits _{x \to 1+0}(x^2-2)=-1\\\\f(1)=(-x)\Big|_{x=1}-1\\\\\lim\limits _{x \to 1-0}f(x)=\lim\limits _{x \to 1+0}f(x)=f(2)=-1\ \ \ \Rightarrow$

При х=1 функция непрерывна.

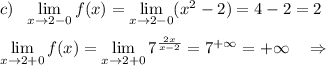
$c)\ \ \lim\limits _{x \to 2-0}f(x)=\lim\limits _{x \to 2-0}(x^2-2)=4-2=2\\\\\lim\limits _{x \to 2+0}f(x)=\lim\limits _{x \to 2+0}7^{\frac{2x}{x-2}}=7^{+\infty }=+\infty \ \ \ \Rightarrow$

При х=5 функция имеет разрыв 2 рода .

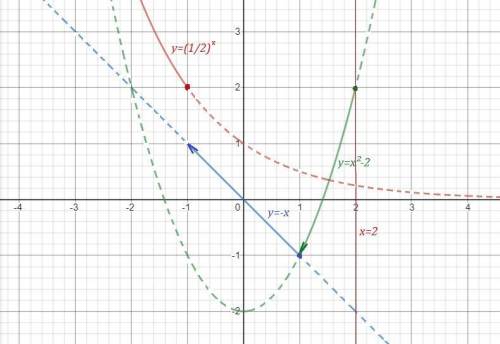
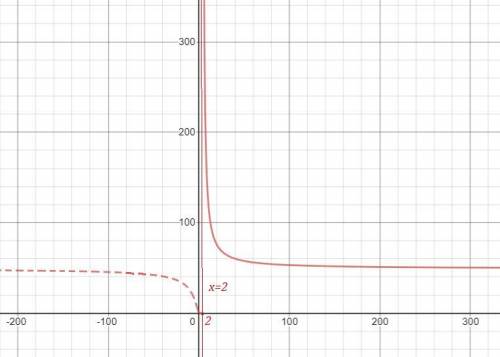
График функции нарисован сплошными линиями.

На 1 рисунке нет чертежа функции при х>2 , для которого прямая х=2 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>2 сплошной линией..

Задана функция f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.

4,4(38 оценок)

Ответ:

alexaval1980p08mu0

08.06.2023

1. Найдём дискриминант данного уравнения.

Наше уравнение вида $a{x}^{2}+2kx+c=0$ , значит будет проще найти дискриминант по 2 формуле: $D={k}^{2}-ac$ (где k=a=1 , c=-80 ).

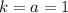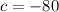$D={1}^{2}-1\cdot(-80)=1-(-80)=1+80=81$ 2. Определим кол-во корней в уравнении.

Вспоминаем правила дискриминанта:

Если дискриминант больше нуля, то уравнение имеет 2 корня.Если дискриминант меньше нуля, то уравнение не имеет корней.Если дискриминант равен нулю, то уравнение имеет 1 корень.

Найденный дискриминант больше нуля 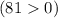(810) , поэтому данное уравнение имеет 2 корня.

3. Найдём определённое кол-во корней уравнения.

Формула корня(-ей) такова: 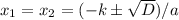${x}_{1}={x}_{2}=(-k\pm \sqrt{D})/a$

(где 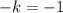-k=-1 , D=81 , a=1 ).

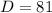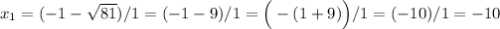
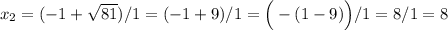${x}_{1}=(-1-\sqrt{81})/1=(-1-9)/1=\Big(-(1+9)\Big)/1=(-10)/1=-10$ ${x}_{2}=(-1+\sqrt{81})/1=(-1+9)/1=\Big(-(1-9)\Big)/1=8/1=8$ 4. Запишем окончательный ответ:

Корни данного уравнения: 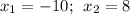${x}_{1}=-10; \: \: {x}_{2}=8$ .