по теореме Виета
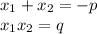
по уравнению р=4, а значит -р = -4
тогда
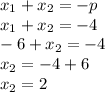
по той же теореме
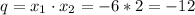
исходное уравнение выглядит
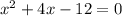
В решении.
Объяснение:
Доказать тождество.
1)2х²(4x²-3)(3+4х²)=32х⁶-18х²
2)3х²(2х²+5)(5-2х²)=75х³-12х⁷
Доказать тождество - значит преобразовать (решить) левую часть, если после преобразования обе части равны, тождество доказано.
1)2х²(4x²-3)(3+4х²)=32х⁶-18х²
В скобках развёрнута разность квадратов, свернуть:
2х² * (4x² - 3)(3 + 4х²) = 2х² * (4x² - 3)(4х² + 3) =
= 2х² * (16х⁴ - 9) = 32х⁶ - 18х² (левая часть).
32х⁶ - 18х² = 32х⁶ - 18х², тождество доказано.
2)3х²(2х²+5)(5-2х²)=75х³-12х⁷
В скобках развёрнута разность квадратов, свернуть:
3х² * (2х² + 5)(5 - 2х²) = 3х² * (5 + 2х²)(5 - 2х²) =
= 3х² * (25 - 4х⁴) = 75х² - 12х⁶ (левая часть).
75х² - 12х⁶ ≠ 75х³-12х⁷, выражение не является тождеством.
Воспользуемся т. Виета
x₁+x₂=-p
x₁*x₂=q
коэффициент р нам известен из уравнения p=4
Мы знаем, что один из корней равен -6 пусть это будет x1 подставим известные значения в формулу x₁+x₂=-p и найдем x₂
-6+x₂=-4
x₂=-4+6=2 подставим х₁ и х₂ в формулу x₁*x₂=q и найдем q
-6*2=-12
q=-12