На определение вероятности. в партии из 15 изделий 12 стандартны. какова вероятность того, что: а) одна наудачу выбранная деталь стандартна; б) из двух наудачу взятых деталей одна стандартна, другая нестандартна? с объяснением
Например для такого рода задач: задача Найдите сумму всех двузначных чисел, которые при делении на 4 дают в остатке 3
наименьшее такое двузначное -- первый член прогрессии находим (в виду небольшого делителя) достаточно легко перебором 10- наименьшее двузначное число 10:4=2(ост 2) 11:4=2(ост 3) 11 - первый член прогрессии (либо оценивая по общей формуле с нахождения наименьшего(наибольшего) натурального удовлетворяющего неравенство так как при делении на 4 остаток 3 общая форма 4k+3 4k+3>=10 4k>=10-3 4k>=7 4k>=7:4 k>=1.275 наименьшее натуральное k=2 при k=2: 4k+3=4*2+3=11 11 -первый член )
далее разность прогрессии равна числу на которое делим т.е. в данном случае 4
далее ищем последний член прогрессии 99- наибольшее двузначное 99:4=24(ост3) значит 99 - последний член прогрессии (либо с оценки неравенством 4l+3<=99 4l<=99-3 4l<=96 l<=96:4 l<=24 24 - Наибольшее натуральное удовлетворяющее неравенство при l=24 : 4l+3=4*24+3=99 99- последний член прогрессии ) далее определяем по формуле количество членов и находим сумму по формуле ответ: 1265
Всего 15 деталей. Из них 12 стандартных,
значит количество нестандартных деталей равно 15-12=3
Вероятность - это отношение числа благоприятных исходов к общему числу исходов.
а) Число благоприятных исходов равно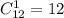
(выбираем одну деталь из 12-ти стандартных)
Общее число исходов равно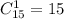
Получаем вероятность события Р=12/15=4/5=0,8 (80%)
б) Число благоприятных исходов равно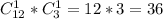
(одну деталь берём из 12-ти стандартных и одну из трёх нестандартных.
Ставим между ними знак умножения, т.к. он заменяет нам союз "и")
Общее число исходов равно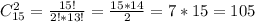
Получаем вероятность события Р= 36/105=12/35 = 0,343 (34,3%)