у = х³ - 3х
у¹ = 3х² - 3
3х² - 3 = 0
х₁ = 1
х₂ = - 1
Это могут быть точки минимума и максимума функции.
Найдем значение производной на всех трех интервалах
х < -1 -1 < х < 1 и x > 1
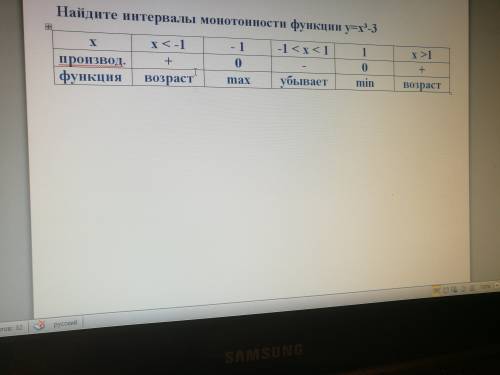
Внесем данные в таблицу (на фото).
Получим, на промежутке (-∞; -1) функция возрастает ,
На промежутке (- 1 ; 1) функция убывает
И на промежутке ( 1 ; + ∞) функция снова возрастает
в точке х= - 1 функция имеет максимум
в точке х = 1 функция имеет минимум.
Это и есть интервалы (или промежутки) монотонности функции
Если при делении задуманного числа на 7 остаток тоже делится на 7, то и все число делится на 7.
Рассуждая аналогично, получается, что это же число делится и на 8, и на 9.
Найдём наименьшее общее кратное для чисел 7; 8; 9.
7 · 8 · 9 = 504
Оказалось, что 504 - трехзначное число, это соответствует условию.
Проверим:
504 - 7 = 497 => 497:7=71 (делится без остатка)
504 - 8 = 496 => 496:8=62 (делится без остатка)
504 - 9 = 495 => 495:9=55 (делится без остатка)
ответ: 504
Перевод
Якщо при діленні задуманого числа на 7 залишок теж ділиться на 7, то і все число ділиться на 7.
Міркуючи аналогічно, виходить, що це ж число ділиться і на 8, і на 9.
Знайдемо найменше спільне кратне для чисел 7; 8; 9.
7 · 8 · 9 = 504
Виявилося, що 504 - тризначне число, це відповідає умові.
Перевірити:
504 - 7 = 497 => 497:7=71 (ділиться без залишку)
504 - 8 = 496 => 496:8=62 (ділиться без залишку)
504 - 9 = 495 => 495:9=55 (ділиться без залишку)
Відповідь: 504
1) 2cos 5п/6 + tg п/3 = 2cos(п-п/6) + tg п/3 = -2cosп/6 + tg п/3 = -√3 + √3 = 0
2) sin(п-a) = √2/2
sina = √2/2
sin^2 a + cos^2 a = 1
0,5 + cos^2 a = 1
cos^2 a = 0,5
cos2a = cos^2 a - sin^2 a = 0,5 - 0,5 = 0
3) ctg^2 a + cos^ a - 1/sin^2 a
(ctg^2 a * sin^2 a + cos^2 a * sin^2 a - 1) / sin^2 a
(cos^2 a + cos^2 a * sin^2 a - 1) / sin^2 a
(cos^2 a * sin^2 a - sin^2 a) / sin^2 a
sin^2 a * (cos^2 a - 1) / sin^2 a
cos^2 a - 1 = -sin^2 a
В четвертом я немного не догоняю сам пример: где должно быть деление и т.д.