Пусть скорость пешехода х км/ч, а велосипедиста — (х+10) км/ч. Пусть встреча произошла на расстоянии у от В. АВ = 4 км - по условию, ВС=у.
АСВ
велосипедист проехал АВ+ВС = 4+у за время (4+у) /х+10,
а пешеход АВ - ВС = 4-у за время (4-у) /х, что равно 24 мин = 2/5 часа.
Система: (4+у) /x+10 = 2/5,
(4-y) / x = 2/5. Запиши в виде дробей и перемножь накрест, как в пропорциях.
Найди у.
2х=20-5у (1) х=20-5у/2
(2) 2х+20=20+5у
Из (1) в (2) подставим 20-5у/2 вместо х:
(2): 2(20-5у/2)+20=20+5у
10у=20
у= 2
подставляем 2 в (1)
х=20-10/2=5 км/ч
скорость пешехода
Объяснение:
1) представьте систему в матричной форме
2) умножьте строку 1на (-2) и прибавить результат к строке 2
Умножьте строку 1на (-1) и прибавить результат к строке 3:
3) умножьте вторую строку на -1
4) умножить строку 3 на 2 и прибавить результат к строке 1.
Умножьте строку 3 на 5 и прибавьте результат к строке 2
5) разделить строку 2 на 14
6) умножить строку 2 на -7 и прибавить результат к строке 1.
Умножить строку 2 на -2 и прибавить результат к строке 3
7) умножить строку 3 на -1
8) преобразовать расширенную матрицу систему линейных уравнений
ответ: решение систем уравнений является упорядоченная тройка (х,у,z)
Решение на фотке

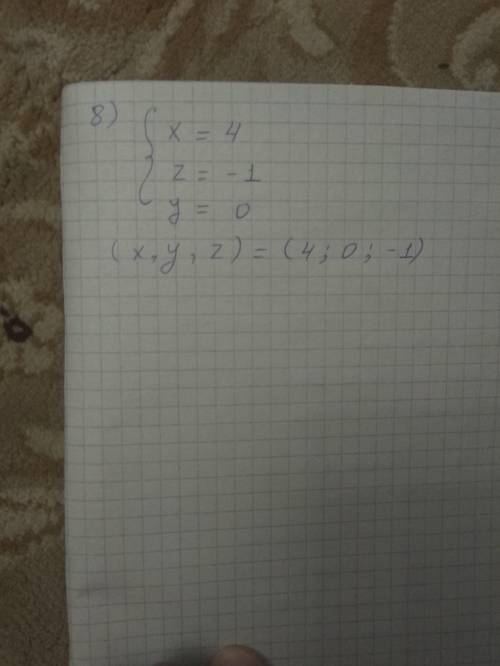
tgx= -0,5 в интервале х∈(-1;1)
1 радиан ≈ 57,2°
х = arctg(-0.5) + πn
x = -arctg(0.5) + πn
n = 0, x = -arctg(0.5), 0>х>-30°, х∈(-1;1)
n = -1 x = -arctg(0.5) - π, -180°>х, х∉(-1;1)
n = 1 x = -arctg(0.5) + π, х>90°, х∉(-1;1)
ответ: x = -arctg(0.5)