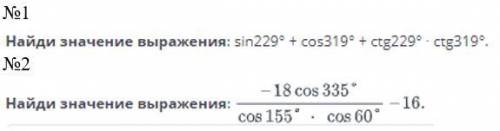
Найди значение выражения: sin229° + cos319° + ctg229° - ctg319.

Найди значение выражения: -18 cos 335°/cos155° • cos 60° - 16

Найди значение выражения: sin229° + cos319° + ctg229° - ctg319.Найди значение выражения: -18 cos 335

👇

Увидеть ответ

Ответ:

marina8marta

26.10.2021

1)sin229° + cos319° + ctg229° * ctg319°=

=sin229°+cos(90°+229°)+ctg(49°+180°)*ctg(139°+180°)

Используя формулу cos(90°+t)=-sint, преобразуем выражение cos(90°+229°)=

=-sin229°

Упростим ctg(49°+180°)=ctg49° и

ctg(139°+180°)=ctg139° ,используя

ctg=(t+k*180°)=ctgt ,где k принадлежит z

В итоге получаем:

sin229°-sin229°+ctg49° * ctg139°=

=ctg49° * ctg139°≈-1

2)( -18cos335°/cos155°*cos60° )-16=

=( -18cos(180°+155°)/cos155°*1/2 )-16=

=( -18cos*(-cos155°)/cos155°*1/2 )-16=

=( -18*-1 / 1*1/2 )-16=( 18/ 1/2 )-16=

=36-16=20

4,8(9 оценок)

Открыть все ответы

Ответ:

евген1398

26.10.2021

РешениеЗадание #1.

с дискриминанта - 8 класс).

Решим квадратное уравнение через дискриминант. Если 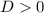, то уравнение имеет 2 корня, если 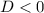, то уравнение не имеет корней. (Если 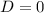D=0 , то уравнение имеет 1 корень)

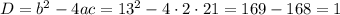
$D=b^2-4ac=13^2-4\cdot2\cdot21=169-168=1$

Поскольку 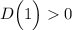$D\Big(1\Big) 0$ , то данное квадратное уравнение имеет 2 корня. Найдём эти корни по формуле.

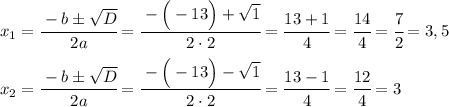
$x_1=\cfrac{-b\pm \sqrt{D}}{2a}=\cfrac{-\Big(-13\Big)+\sqrt{1}}{2\cdot2}=\cfrac{13+1}{4}=\cfrac{14}{4}=\cfrac{7}{2}=3,5 \\ \\ x_2=\cfrac{-b\pm \sqrt{D}}{2a}=\cfrac{-\Big( -13\Big)-\sqrt{1}}{2\cdot2}=\cfrac{13-1}{4}=\cfrac{12}{4}=3$

с группировки - 7 класс).

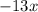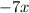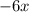Представим число -13x в виде двух чисел: -7x и -6x . А затем сгрупируем по два члена в скобки и вынесен за скобки общий множитель.

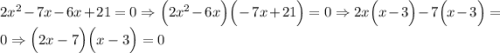
$2x^2-7x-6x+21=0 \Rightarrow \Big(2x^2 -6x\Big) \Big(-7x+21\Big)=0 \Rightarrow 2x\Big(x-3\Big)-7\Big(x-3\Big)=0 \Rightarrow \Big(2x-7\Big)\Big(x-3\Big)=0$

По правилу если произведение равно нулю, то хотя бы один из данных множителей будет равняться нулю. Рассмотрим 2 единственных случая.

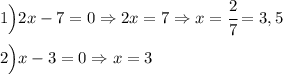
$1\Big) 2x-7=0 \Rightarrow 2x=7 \Rightarrow x=\cfrac{2}{7}=3,5 \\ \\ 2\Big) x-3=0 \Rightarrow x=3$

ответ: $\boxed{\bf x_1=3,5; \: \: x_2=3}$ .Задание #4.

с дискриминанта - 8 класс).

Для начала нужно в правой части уравнения умножить многочлен на многочлен, а затем перенести все члены из правой части в левую со сменой знака, а в правой части поставим .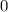

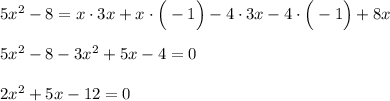
$5x^2-8=x\cdot3x+x\cdot\Big(-1\Big)-4\cdot3x-4\cdot\Big(-1\Big)+8x\\ \\ 5x^2-8-3x^2+5x-4=0 \\ \\ 2x^2+5x-12=0$

Найдём дискриминант данного квадратного уравнения. Если 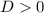, то уравнение имеет 2 корня, если 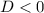, то уравнение не имеет корней. (Если 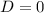D=0 , то уравнение имеет 1 корень)

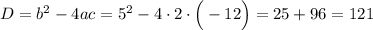
$D=b^2-4ac=5^2-4\cdot2\cdot\Big(-12\Big)=25+96=121$

Поскольку 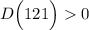$D\Big(121\Big) 0$ , то данное квадратное уравнение имеет 2 корня. Найдём эти корни по формуле.

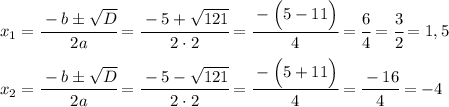
$x_1=\cfrac{-b\pm \sqrt{D}}{2a}=\cfrac{-5+\sqrt{121}}{2\cdot2}=\cfrac{-\Big(5-11\Big)}{4}=\cfrac{6}{4}=\cfrac{3}{2}=1,5 \\ \\ x_2=\cfrac{-b\pm \sqrt{D}}{2a}=\cfrac{-5-\sqrt{121}}{2\cdot2}=\cfrac{-\Big(5+11\Big)}{4}=\cfrac{-16}{4}=-4$

с группировки - 7 класс).

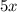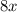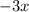Представим число в виде двух чисел: и -3x . А затем сгрупируем по два члена в скобки и вынесен за скобки общий множитель.

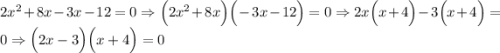
$2x^2+8x-3x-12=0 \Rightarrow \Big(2x^2+8x\Big)\Big(-3x-12\Big)=0 \Rightarrow 2x\Big(x+4\Big)-3\Big(x+4\Big)=0 \Rightarrow \Big(2x-3\Big)\Big(x+4\Big)=0$

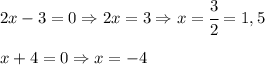
$2x-3=0 \Rightarrow 2x=3 \Rightarrow x=\cfrac{3}{2}=1,5 \\ \\ x+4=0 \Rightarrow x=-4$

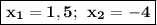ответ: $\boxed{\bf x_1=1,5; \: \: x_2=-4}$ .Задание #7.

Сделаем из данного уравнения систему и найдём дискриминант каждого нового уравнения. Если 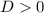, то уравнение имеет 2 корня, если 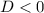, то уравнение не имеет корней. (Если 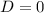D=0 , то уравнение имеет 1 корень)

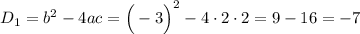
$D_1=b^2-4ac=\Big(-3\Big)^2-4\cdot2\cdot2=9-16=-7$

Т.к. 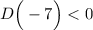$D\Big(-7\Big)$ , то данное уравнение НЕ ИМЕЕТ КОРНЕЙ! Теперь находим дискриминант второго квадратного уравнения:

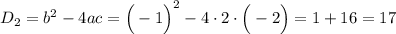
$D_2=b^2-4ac=\Big(-1\Big)^2-4\cdot2\cdot \Big(-2\Big)=1+16=17$

Т.к. 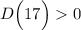$D\Big(17\Big)0$ , то данное уравнение имеет 2 корня. Решим данное уравнение по формуле.

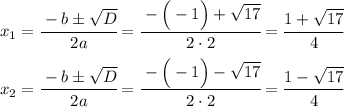
$x_1=\cfrac{-b\pm \sqrt{D}}{2a}=\cfrac{-\Big(-1\Big)+\sqrt{17}}{2\cdot2}=\cfrac{1+\sqrt{17}}{4} \\ \\ x_2=\cfrac{-b\pm \sqrt{D}}{2a}=\cfrac{-\Big(-1\Big)-\sqrt{17}}{2\cdot2}=\cfrac{1-\sqrt{17}}{4}$

ответ: уравнение имеет 2 корня.Задание #9.

Сначала находим неизвестный множитель, деля произведение на известный множитель, а затем находим корень(-и) данного уравнения.

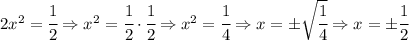
$2x^2=\cfrac{1}{2} \Rightarrow x^2=\cfrac{1}{2}\cdot \cfrac{1}{2} \Rightarrow x^2=\cfrac{1}{4} \Rightarrow x=\pm \sqrt{\cfrac{1}{4}} \Rightarrow x=\pm \cfrac{1}{2}$

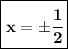
ответ: $\boxed{\bf x=\pm \cfrac{1}{2}}$

4,6(53 оценок)

Ответ:

anzoroglyan1

26.10.2021

Боковые стороны по определению равны (т.к. они равнобедренные)
1. Нужно опустить перпендикуляр к большему основанию (от любого конца меньшего основания (концов всего 2 ))
2. Из за опущенного перпендикуляра образуется прямоугольный треугольник, гепотенуза которого равна 5 корней из 2 и углом 45 градусов. Из этого треугольника мы можем высчитать как высоту трапеции, так и отрезок большего основания. И т.к. у нас образовался прямоугольный треугольник, то 2 катета будут равными ( 2 угла по 45 градусов, один 90). Если посчитать, то действия будут примерно такими: Возьмём за х одну из 2ух равных сторон ( какую бы мы не взяли, разницы нету, они равные), и получаем пропорцию (и ещё, sin45=cos45=корень из 2 делённый на 2)
√(2)/2=x/5√2 => x=5 (синус - противолежащий катет на гипотенузу, косинус - прилежащий катет на гипотенузу)
3. Мы нашли высоту и часть большего основания, далее мы найдём всё большее основания. Так как трапеция равнобедренная, то отрезки будут с разных концов равными друг для друга => Большее основание= 10+5*2=20
4. Ну а теперь находим площадь. Площадь трапеции расчитывается по формуле: S=Средняя линия трапеции*H. Средняя линия трапеции расчитывается по формуле Ac=(большее основание + меньшее основание)/2. S=(20+10)2*5=> S=75
Надеюсь я сумел вам

4,8(48 оценок)

Это интересно:

Компьютеры-и-электроника

28.03.2021

Как удалить историю веб поиска в Google: простые шаги для защиты вашей конфиденциальности...

Компьютеры-и-электроника

27.03.2021

Как поймать Суикуна в игре Покемон - Кристальная версия...

Образование-и-коммуникации

07.08.2020

Как нарисовать собачью морду: советы и инструкции...

Компьютеры-и-электроника