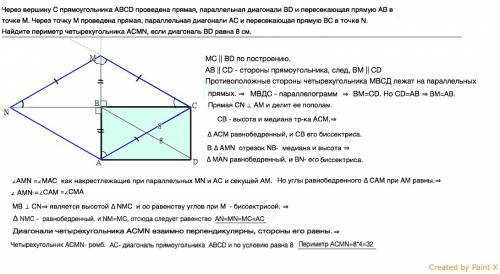
Через вершину C прямоугольника ABCD проведена прямая, параллельная диагонали BD и пересекающая прямую AB в точке M. Через точку M проведена прямая, параллельная диагонали AC и пересекающая прямую BC в точке N. Найдите периметр четырехугольника ACMN, если диагональ BD равна 8 см
–––––––––––––––
Казалось бы очевидно- стороны четырехугольника ACMN равны между собой и равны диагоналям прямоугольника. Тем не менее это нужно доказать.
МС║ВD по построению.
АВ║ СD - стороны прямоугольника, след, ВМ║СD
Противоположные стороны четырехугольника МВСД лежат на параллельных прямых. ⇒
МВДС - параллелограмм.⇒
ВМ=СD. Но СD=АВ ⇒ ВМ=АВ.
СN ⊥ АМ и делит ее пополам. СВ - высота и медиана ∆ АСМ,⇒
∆ АСМ равнобедренный, и СВ его биссектриса.
В ∆ АМN отрезок NB – медиана и высота ⇒
∆ МАN равнобедренный, и BN- его биссектриса.
AN= MN, a MN=MC=AC
∠АМN =∠MАС как накрестлежащие при параллельных МN и АC и секущей АМ.
Но углы равнобедренного ∆ САМ при АМ равны.⇒∠ АМN=∠СМА=∠САМ ,
МВ ⊥ СN⇒ является высотой ∆ NMC и оо равенству углов при М - биссектрисой. ⇒
NMC - равнобедренный, и NM=MC, отсюда следует равенство AN=MN=MC=АС
Четырехугольник АСМN- ромб.
АС- диагональ прямоугольника ABCD и по условию равна 8
Периметр АСМN=8*4=32
Объяснение:
Пусть ограничений нет. Тогда число переставить буквы в слове СССМП равно 9!4!3!1!1!=2520 (перестановки с повторениями).
Предположим, что все 4 буквы И идут подряд. Тогда можно из них образовать новый "комбинированный" символ [И], и получится набор символов СССМП[И], откуда по той же формуле число перестановок окажется равно 6!/3!=120.
Теперь объединим в новый "символ" 3 буквы И, а одну оставим в стороне. "Символов" станет 7, из них С встречается 3 раза, а остальные по одному. Перестановок получается 7!/3!=840. Каждое из 120 буквосочетаний, в котором все 4 буквы И следуют подряд, учитывается два раза: когда мы группируем первые три, и когда группируем последние три буквы И из четырёх. Значит, расположений с тремя И подряд будет 840−120=720, так как 120 были учтены два раза вместо одного.
Окончательно получается 2520−720=1800.