(х + 2)(х - 2) - (х + 2)^2=x^2-4-(x^2+4x+4)=x^2-4-x^2-4x-4=-4x-8=-4(x+2)
По моему
б) и в)
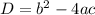 (если дискриминант больше нуля уравнение имеет 2 корня, если равен нулю, уравнение имеет 1 корень, если меньше нуля, то нет корней), либо применяя разложение многочлена
(если дискриминант больше нуля уравнение имеет 2 корня, если равен нулю, уравнение имеет 1 корень, если меньше нуля, то нет корней), либо применяя разложение многочлена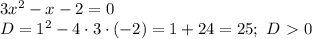
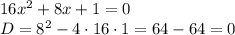


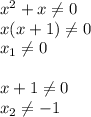
1) (х + 2)(х - 2) - (х + 2)^2
(х + 2)(х - 2)=x^2 - 4, а (х + 2)^2= x^2+4x+4 Поетому
(х + 2)(х - 2) - (х + 2)^2 = 0
x^2 - 4 - x^2 - 4x - 4 = 0
-4x - 8=0
-4x = 8
x = -2
Відповідь: -2
2) Б, В, Г