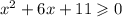
Основное правило: все неравенства, в которых присутствует множитель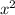 
решаются только методом интервалов. Также только методом интервалов решаются дробные неравенства, если неизвестный множитель стоит в знаменателе.
1) Определим ОДЗ (область допустимых значений):
(
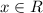— любое число).
2) Приравняем неравенство к нулю и находим корни уравнения:
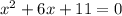
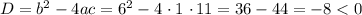
Если дискриминант меньше нуля, то парабола, которая исходит из данного уравнения не имеет общих точек с осью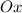 
и, благодаря тому, что 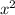положительный, то парабола будет находиться в положительных координатах оси ординат (ось 
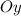). В таком случае, при любом значении икса неравенство будет иметь смысл (потому что в нашем неравенстве стоит знак 
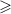, что правильно со значением уравнения. Если бы в таком неравенстве стоял бы знак 
или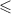 
, то такое неравенство не имело бы смысла, так как сама парабола находиться в положительных значениях оси ординат).
ответ: 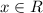( — любое число).
Область определения (обозначается D(y)) функции находится следующим образом. Необходимо проанализировать функцию на наличие корней, знаменателей и логарифмов. Последний случай нас мало интересует, потому сразу перейдем к двум первым.
А именно: в знаменателе не должен быть ноль, а число под корнем не должно быть отрицательным.
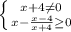
На самом деле, первую строчку можно опустить, далее поймете почему).
Решая вторую строчку получаем:
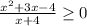
Из этого следует, что x1≠-4, x2=-4, x3=1 (2 и 3 корни получились путем решения квадратного уравнения в числителе).
Далее методом интервалов находим промежутки, удовлетворяющие условию ≥0. Таким промежутком является [1;∞).
ответ: D(y)=[1;∞)
Объяснение:
y=x²+x-20
f(5)=5²+5-20=10
f(4)=4²+5-20=1
(k;-8)
x²+x-20=-8
x²+x-12=0
D=1-4*(-12)=49
x1=(-1+7)/2=3
x2=(-1-7)/2=-4
k1=3
k2=-4