Решение: Необходимо найти все двузначные числа, пр перестановки которых число увеличится на 9. Введем некоторые понятия: Пусть - это число десятков, а - число единиц. Тогда, если цифры в числе поменять соответственно, получим: . Исходя из наших суждений, получим следующее уравнение: Попробуем максимально упростить уравнение: Следовательно, мы получили исходное условие: разность двух чисел обязательно равна минус единице. Теперь, найдем все двузначные числа, при перемене которых даст число, большее на 9. Это: 12, 23, 34, 45, 56, 67, 78, 89. ответ: 12, 23, 34, 45, 56, 67, 78, 89
- это число десятков, а 
- число единиц. Тогда, если цифры в числе поменять соответственно, получим: 
. Исходя из наших суждений, получим следующее уравнение:
1) a)y=3 б)x=3 в) (3;+∞) возрастает (-∞;3) убывает
2)а)у=-0,5 б) у=0,25 в) у=3
3) у(4)>y(3) y(-3)>y(-2) y(2)<y(-5)
Объяснение:
1) находим по графику абсцисса -это х ордината это -у
2)подставляем вместо х значение и считаем
3) a)у(4)=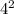
=16 б)у(-3)=
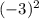=9 в) у(2)=
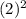=4
у(3)=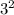
=9 у(-2)=
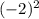=4 у(-5)=
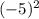=25
у(4)>y(3) y(-3)>y(-2) y(2)<y(-5)