Объяснение:
Для того, чтобы вычислить площадь фигуры, ограниченной данными линиями, мы сперва должны построить их на графике
Теперь мы видим, что функцией y = 0, наша искомая фигура разбивается на две симметричные. Их площадь будет равна, то есть для того, чтобы вычислить площадь фигуры, нам достаточно найти площадь одной её половины и умножить на "2".
Получается, площадь равна удвоенному интегралу функции х^3 от 2 до 0.
2 * инт (х^3)dx = 2 * (x^4)/4.
Подставляем наши границы "2" и "0": 2 * (x^4)/4 = 2 * ((2^4)/4 - (0^4)/4) = 2 * 4 = 8.
ответ: S фигуры = 8.
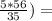log₂8 = 3
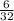= log₂(
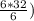= log₂32 = 5
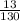= lg
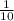= -1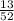
)⁵ = (log₂
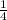)⁵ = (-2)⁵ = -32
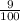)⁴ = (log₀.₃0.09)⁴ = 2⁴ = 16
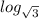log₅125 = 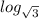3 = 2
ответ:37
Объяснение: 180 - (114+29) = 37