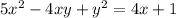
Преобразуем уравнение:
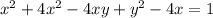
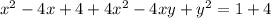
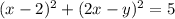
Если  и
и 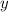 - целые числа, то и выражения
- целые числа, то и выражения  и
и 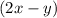 также являются целыми.
также являются целыми.
Тогда, выражения 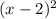 и
и 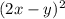 соответствуют квадратам целых чисел.
соответствуют квадратам целых чисел.
Если 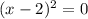 , то
, то 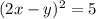 - но число 5 не является квадратом
- но число 5 не является квадратом 
целого числа, поэтому этот вариант не реализуется.
Если 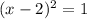 , то
, то 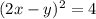 .
.
Если 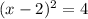 , то
, то 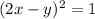 .
.
Если 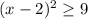 , то
, то 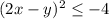 - эти варианты также не реализуются, так как квадрат числа не может быть отрицательным.
- эти варианты также не реализуются, так как квадрат числа не может быть отрицательным.
Таким образом, нужно рассмотреть два случая.
Первый случай:
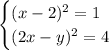
Такую систему можно расписать в виде совокупности четырех систем. Запишем в виде краткого условия:
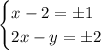
Из первого условия получим:
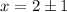
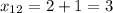
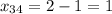
Из второго условия получим:
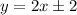
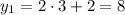
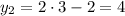
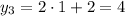
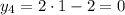
Таким образом, найдены решения:
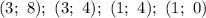
Второй случай:
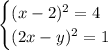
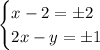
Из первого условия получим:
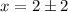
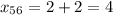
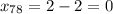
Из второго условия получим:
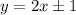
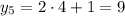
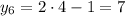
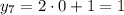
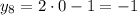
Таким образом, найдены решения:
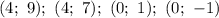
Последняя пара чисел не удовлетворяет условию о том, что решения должны быть составлены из неотрицательных чисел. Эта пара чисел не идет в ответ.
ответ: 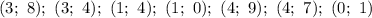
f'' (x) = 3x^2+6x = 0
3x(x+2)=0
x=0, x= -2
Рисуешь координатную прямую, на ней отмечаешь эти две точки. Они делят прямую на 3 промежутка: на первом промежутке(-бесконечность; -2] ставь плюс на втором минус, на третьем тоже плюс. Таким образом, а) функция убывает на промежутке от (-бесконечность; -2], возрастает от [-2; +бесконечность)...б) -2 точка минимума, 0 не является точкой экстремума, т.к. там не происходит смена знака...в) чтобы найти наибольшее и наименьшее значение, ты должен подставить -4, -2, 0 и 1 в начальную функцию и посчитать.