1. Решите задачу с уравнения: Площадь прямоугольника, одна из сторон которого на 14смменьше другой, равна 32 м2.Найдите стороны и периметр прямоугольника.
2. Запишите координаты вершины параболы, укажите направление ее ветвей и постройте график функции y = x2 – 2x – 3.По графику определите нули функции, ось симметрии, промежутки возрастания и убывания, наибольшее и наименьшее значение функции.
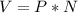
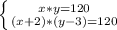

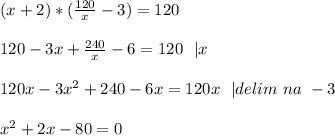
(х-3+1)/(х+1) = (х-2)/(х+1) - новая дробь
Так как по условию их разность равна 3/20, то составляем уравнение:
(х-2)/(х+1) - (х-3)/ х = 3/20
приводим к общему знаменателю: 20х(х+1) и отбрасываем его, заметив, что х≠0, х≠-1
20х(х-2)-20(х+1)(х-3) = 3х(х+1)
20х²-40х-20х²+40х+60=3х²+3х
3х²+3х-60=0 | :3
х²+х-20=0
Д=1+80=81=9²
x(1)=(-1+9)/2=4 => исходная дробь (4-3) / 4 = 1/4
x(2)=(-1-9)/2=-5 => исходная дробь (-5-3) / (-5) = -8/(-5) = 8/5>1 не подходит под условие задачи
ответ: 1/4