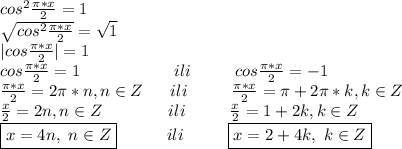
Теперь корни принадлежащиепромежутку
![[\pi;3\pi]\approx[3.14;9.42]\\x=4n,n\in Z\\n=1;x=4\\n=2;x=8\\\\x=2+4k,k\in Z\\k=1;x=2+4=6](/tpl/images/0172/0113/b620a.png) [/tex]
[/tex]
4*8*6=192
Будут вопросы пишив личку.
Пусть за  час 1-й кран будет наполнять весь бассейн
час 1-й кран будет наполнять весь бассейн
за 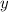 час 2-й кран будет наполнять бассейн.
час 2-й кран будет наполнять бассейн.
Если 1 - это объем всего бассейна, тогда
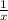 - объем воды, который проходит через 1-й кран за 1 час.
- объем воды, который проходит через 1-й кран за 1 час.
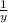 - объем воды, который проходит через 2-й кран за 1 час.
- объем воды, который проходит через 2-й кран за 1 час.
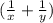 - общая производительность двух кранов.
- общая производительность двух кранов.
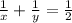 - первое уравнение
- первое уравнение
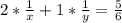 - второе уравнение
- второе уравнение
Из первого уравнения получим: 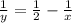 и вставим во второе уравнение:
и вставим во второе уравнение:
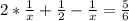
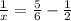
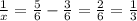
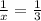
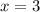
Подставим 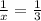 в первое уравнение:
в первое уравнение:
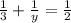
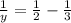

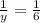
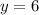
ответ: за 3 часа 1-й кран наполнит весь бассейн;
за 6 часов 2-й кран наполнит весь бассейн.
Для функции y(x)=x²-4x+3 найдите:
1 область определения функции;
2 множество значений функции;
3 наименьшее (наибольшее) значение функции;
4 уравнение оси симметрии параболы:
5 нули функции;
6 промежутки знакопостоянства функции;
7 промежутки монотонности функции
Объяснение:1. Область определения (-∞; +∞).
2. Область значений [-1; +∞).
3. Минимальное значение f(x) принимает в точке xmin = 2, f(2) = -1.
4. Ось симметрии x=2.
5. Нули функции x1=1, x2=3.
6. f(x)>0, при х∈(-∞;1)∪(3;+∞).
f(x)<0, при х∈(1;3).
7. f(x) убывает при х∈(-∞;2), f(x) возрастает при х∈(2;+∞).
Для функции y(x)=x²-4x+3 найдите:
1) область определения функции;
2)множество значений функции;
3)наименьшее (наибольшее) значение функции;
4)уравнение оси симметрии параболы:
5)нули функции;
6)промежутки знакопостоянства функции;
7)промежутки монотонности функции
на промежутке![[\pi;3*\pi]](/tpl/images/0172/0113/94d71.png) решениями данного уравнения есть 4,6,8
решениями данного уравнения есть 4,6,8
их произведение 4*6*8=192