ответ: 21 см
Объяснение:
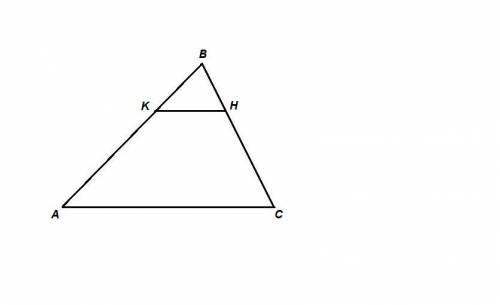
Дано: ΔАВС, КН║АС, Sakh : Sakhc = 1 : 8
Pakh = 7 см
Найти: Pabc.
Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Sakh : Sakhc = 1 : 8, значит площадь треугольника АВС составляет 9 частей, тогда
Sakh : Sabc = 1 : 9 = k²
k = 1/3
Отношение периметром подобных треугольников равно коэффициенту подобия:
Pakh : Pabc = 1 : 3
Pabc = Pakh · 3 = 7 · 3 = 21 см
2x-3=5-2x
2x+2x=5+3
4x=8
x=8/4
x=2
2x+1=3-x
2x+x=3-1
3x=2
x=2/3
x-4=2-3x
x+3x=2+4
4x=6
x=6/4
x=1.5
2x+5=5-x
2x+x=5-5
3x=0
x=0
x-4=4-x
x+x=4+4
2x=8
x=8/4
x=2
2x-8=11-3x
2x+3x=11+8
5x=19
x=19/5
x=3.8
17x+11=6+12x
17x-12x=6-11
5x=-5
x=-5/5
x=-1
11x-4=4-x
11x+x=4+4
12x=8
x=8/12
x=2/3
x-8=11-12x
x+12x=11+8
13x=19
x=19/13
2x-4=5-x
2x+x=5+4
3x=9
x=9/3
x=3
x/2-3x-2/4=3
0.5x-3x=3+0.5
-2.5x=3.5
x=-3.5/2.5
x=-1.4
Начать следует с раскрытия скобок. Скобки (6x+7)(6x-7) можно раскрыть, используя формулу сокращённого умножения (a-b)(a+b)=a^2-b^2. Используем её в уравнении:
(6х+7)(6х-7)+12х=36х^2+12х-49
36x^2-49+12x=36x^2+12x-49
Теперь перенесём все переменные x в левую часть уравнения, а все числа - в правую. Получим:
36x^2+12x-36x^2-12x=-49+49
Приведём подобные слагаемые в обеих частях уравнения, попутно взаимоуничтожив все противоположные слагаемые:
36x^2 и -36x^2 взаимоуничтожились
12x и -12 x тоже взаимоуничтожились
-49 и 49 тоже взаимоуничтожились
Что же мы получаем? В обеих частях уравнения все слагаемые уничтожены, мы получили это:
0=0
Полученное нами равенство оказалось верным.
Это значит, что какое бы мы x ни выбрали, эта переменная всегда будет пропадать и равенство будет верным. Из этого следует, что у данного уравнения бесконечное количество решений.
ответ: x - любое число