Число р при делении на 3 может давать остатки 0,1 или 2.
Если число р при делении на 3 дает остаток 1, то оно имеет вид
p=3k+1, где k - некоторое целое число
Но тогда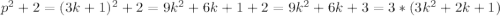 
, а значит число 
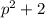не является простым. Значит такой случай невозможен
Если число р при делении на 3 дает остаток 2, то оно имеет вид
p=3k+2, где k - некоторое целое число
Но тогда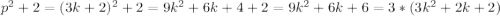 
, а значит число 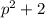не является простым. Значит такой случай невозможен
Значит число р при делении на 3 дает остаток 0, а значит число р делится нацело на 3. Число р делится нацело на 3 и является простым, значит число р может равняться только числу 3.
При р=3: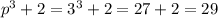 
- простое, что и требовалось доказать.Доказано
Условие написано так, что можно только догадываться о правильном условии.
Скорее всего "е" в степени lnx, а это равно х (если основание степенной ф-ции и основание логарифмической ф-ции, которая записана в показателе,равны, то получим в результате аргумент логар. ф-ции. lnx- это логарифм по основанию "е")
Уравнение перепишется так: 3*х=8х-23
5х=23
х=23/5
х=4,6
ну очевидно что это 6 и 6)
Но попробуем доказать. обозначим первое число через x а второе y
тогда x+y=12
Как известно, x+y>=2sqrt(xy) (больше либо равно 2 корня из xy)
то есть 2sqrt(xy)<=12
sqrt(xy)<=6
xy<=36, то есть наибольшее возможное произвдение x и y =36. 6 и 6 дают именно такой результат