Пусть Sкм весь путь
1/4Sкм путь за 1-й день
2/5Sкм 2-й
По условию задачи составим ур-е
S - (1/4S + 2/5S) = 7
S - 13/20S = 7
7/20S = 7
S = 7: 7/20
S = 7*20/7
S = 20км
Решите уравнение
ОДЗ уравнения: все числа.
Преобразуем уравнение, воспользуемся формулой двойного аргумента cos2x = 2cos2x – 1, получим:
2cos2x – 1 – cosx = 0
2cos2x – cosx – 1 = 0
Введем новую переменную, пусть cosx = a, тогда
2a2 – a – 1 = 0
D = 9
a1 = 1 и a2 = — 1/2
Вернемся к первоначальной переменной, получим 2 уравнения:
cosx = 1 и cosx = — 1/2
Решим 1 уравнение:
cosx = 1
Задание13в21_1
Решим 2 уравнение:
cosx = — 1/2
Задание13в21_2
Задание13в21_3
Все три корня можно объединить в один, для этого воспользуемся единичной окружностью
Задание13в21_4
Из рисунка видно, что корни повторяются через 2π/3, тогда
Задание13в21_5
В решении.
Объяснение:
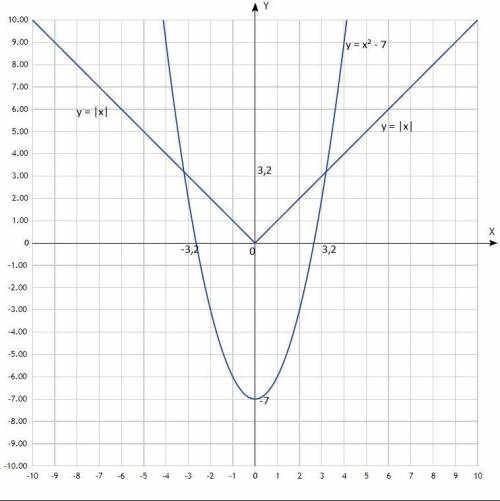
Решить графически систему уравнений:
у = х² - 7
у = |x|
Первый график - парабола со смещённым центром, ветви направлены вверх.
Второй график - график функции модуля (значения у всегда > 0).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х² - 7 у = |x|
Таблицы:
х -4 -3 -2 -1 0 1 2 3 4 х -3 -2 -1 0 1 2 3
у 9 2 -3 -6 -7 -6 -3 2 9 у 3 2 1 0 1 2 3
По вычисленным точкам построить графики.
Согласно графиков, координаты точек пересечения:
(-3,2; 3,2); (3,2; 3,2).
Решения системы уравнений: (-3,2; 3,2); (3,2; 3,2).
за первый и второй день вместе туристы
(1/4) + (2/5) = (5/20) + (8/20) = 13/20 всего пути
значит, осталось пройти
1 - 13/20 = 20/20 - 13/20 = 7/20 всего пути осталось пройти в третий день ---это 7км
7/20 7
чтобы найти целое по его части, нужно число (7) разделить на дробь, обозначающую часть (7/20), получим: 7 / (7/20) = 7 * 20/7 = 20 ---это целое (весь путь)
ПРОВЕРКА:
в первый день пути --- 20*(1/4) = 5(км)
во второй день пути --- 20*(2/5) = 8(км)
осталось пройти 20-5-8 = 7(км) ---верно...