Обозначим cлагаемые за Х,У,Z
(X+Y+Z)/3>=1
Согласно неравенству о среднем арифметическом и среднем геометрическом достаточно доказать :
ХУZ>=1
Вернемся к исходным обозначениям
8abc>=(a+b)(b+c)(a+c)
Снова согласно неравенству о среднем арифметическом и среднем геометрическом видим
a+b>=2sqrt(ab) b+c>=2sqrt(сb) (a+c)>=2sqrt(ac)
поэтому можим заменить сомножители справа на произведение
2sqrt(ab)*2sqrt(aс)*2sqrt(сb)=8abc, что и доказывает неравенство.
Равенство достигается только при а=с=b
Объяснение:
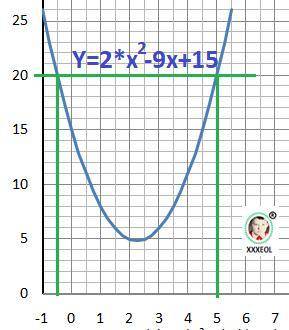
Удаляем знак модуля и превращаем в квадратное уравнение: y =2*x²- 9*x- 5 ≥ 0 - квадратное уравнение.
D = b² - 4*a*c = (-9)² - 4*(2)*(-5) = 121 - дискриминант. √D = 11.
x₁ = (-b+√D)/(2*a) = (9+11)/(2*2) = 20/4 = 5 - первый корень
x₂ = (-b-√D)/(2*a) = (9-11)/(2*2) = -2/4 = -0,5 - второй корень
Это две точки где границы уравнения задачи. Записываем неравенство:
y ≥ 20 при х ∈(-∞;- 0.5]∪[5;+∞)
Наименьшее положительное - х = 5 - ответ.
Рисунок с графиком функции показывает, что отрицательным это выражение не бывает.
V1 = pi * (d/2) ^ 2 * 405
V2 = pi * (d / 2) ^ 2 * 81 * h
h = 405 / 81 = 5
Радиус в квадрат возводится