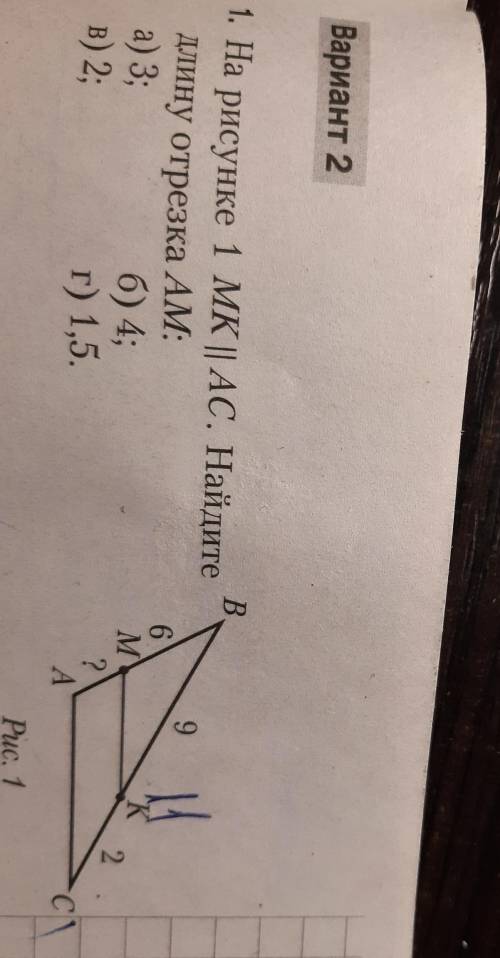
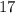 и
и  – среднеарифметическое равно
– среднеарифметическое равно  и при этом
и при этом  на
на  меньше двадцати пяти и на
меньше двадцати пяти и на  больше семнадцати.
больше семнадцати. монет и у них становится поровну, то они как раз и приходят к среднеарифметическому их начальных количеств монет. В итоге у Васи оказывается на
монет и у них становится поровну, то они как раз и приходят к среднеарифметическому их начальных количеств монет. В итоге у Васи оказывается на  монет меньше изначального, а у Пети на
монет меньше изначального, а у Пети на  монет больше изначального. А значит, вначале у Васи было на
монет больше изначального. А значит, вначале у Васи было на 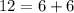 монет больше, чем у Пети.
монет больше, чем у Пети. монет. Тогда у Пети
монет. Тогда у Пети  монет.
монет.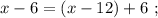
 монет, а у Пети-II будет
монет, а у Пети-II будет  монет. При этом у Пети-II монет в
монет. При этом у Пети-II монет в 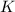 раз меньше, т.е. если мы количество монет Пети-II мысленно увеличим в
раз меньше, т.е. если мы количество монет Пети-II мысленно увеличим в 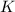 раз, то их станет столько же, сколько и у Васи-II. На этом основании составим уравнение:
раз, то их станет столько же, сколько и у Васи-II. На этом основании составим уравнение:

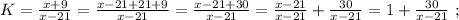

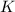 было целым, целой должен быть и результат деления в дроби, а чтобы
было целым, целой должен быть и результат деления в дроби, а чтобы 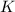 было максимальным, частное от деления в дроби должно быть максимальным, а значит её знаменатель должен быть минимальным, целым, положительным числом, что возможно только, когда
было максимальным, частное от деления в дроби должно быть максимальным, а значит её знаменатель должен быть минимальным, целым, положительным числом, что возможно только, когда 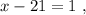 откуда:
откуда:
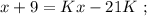

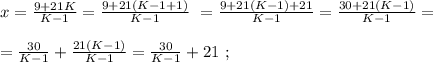
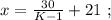
 было целым, целой должен быть и результат деления в дроби. А максимальное значение знаменателя в такой дроби (при том, что частное от деления остаётся целым) составляет
было целым, целой должен быть и результат деления в дроби. А максимальное значение знаменателя в такой дроби (при том, что частное от деления остаётся целым) составляет 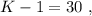 откуда:
откуда:
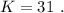
1. Область определения функции
2. Нечетность функции
Функция ни четная ни нечетная...................
3. Точки пересечения с осью Ох и Оу
3.1. С осью Ох
3.2. С осью Оу (х=0)
(0;3) - точки пересечения с осью Оу
Критические точки, возрастание и убывание функции
_____-___(1)_____+_____
Итак, функция возрастает на промежутке x∈ [1;+∞), убывает на промежутке x ∈ (-∞;1]. В точке х=1 функция имеет локальный минимум
Точки перегиба нет так как вторая производная
Горизонтальных, наклонных и вертикальных асимптот нет