Вертикальные асимптоты: x = 2
Горизонтальные асимптоты: y = 3
Нет наклонных асимптот
Объяснение:
Выясним, при каких значениях переменной функция 3 x + 1 x − 2 не определена. x = 2
Рассмотрим рациональную функцию
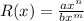, где n - степень числителя, а m - степень знаменателя.
1. Если n < m , то ось x, y = 0 , является горизонтальной асимптотой.
2. Если n = m , то горизонтальной асимптотой является прямая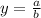 
Если n > m , то не существует горизонтальной асимптоты (только наклонная асимптота).
Найдем n и m
n = 1 ; m = 1
Поскольку n = m , горизонтальная асимптота является прямой 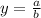, где a = 3 и b = 1
y = 3
Наклонных асимптот нет, поскольку степень числителя меньше либо равна степени знаменателя.
Это множество всех асимптот.
Вертикальные асимптоты: x = 2
Горизонтальные асимптоты: y = 3
Нет наклонных асимптот
вот))
Объяснение:
Решение.
1 этап. Обозначение некоторого неизвестного числа буквой.
Пусть x деталей в день должен был изготавливать цех по плану, (x + 6) деталей в день изготавливал цех ежедневно.
Тогда 24x деталей необходимо изготовить цеху всего.
2 этап. Составление уравнения (математической модели задачи).
Учти условие, что за 4 дня до срока заказ был выполнен, то есть все детали были изготовлены.
Тогда 20(x + 6) деталей, изготовленные цехом за 20 дней, приравняй к общему количеству деталей, равному 24x.
Составь уравнение (математическую модель данной задачи).
20(x + 6) = 24x
3 этап. Решение уравнения.
Реши уравнение.
20(x + 6) = 24x
20x + 120 = 24x
24x – 20x = 120
4x = 120
x = 120 : 4
x = 30 (д) – в день должен был изготавливать цех по плану.
4 этап. Запись ответа в соответствии с условием задачи.
Тогда
24 ∙ 30 = 720 (д) – всего должен был изготовить цех.
ответ: 720 деталей.
Объяснение:
(5с-3д)²-9д²=(5c-3д-3д)(5c-3д+3д)=5c(5c-6д)