1. нет; 2. 1) общего вида 2) общего вида 3) общего вида 3. 1) -1; 3 2) 1; -3 4) -1
Объяснение:
1. Если функция нечетная то произведение f(3)f(-3) не будет положительным.
2.
1)
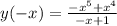
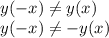
Это функция общего вида
2)
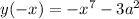
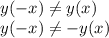
Это функция общего вида
3)
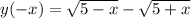
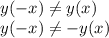
Это функция общего вида
3.
1)
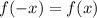
Значит
![min_{[2;4]}f(x)=min_{[-4;-2]}f(x)=-1\\max_{[2;4]}f(x)=max_{[-4;-2]}f(x)=3](/tpl/images/1407/6823/69e2d.png)
2)
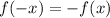
Значит
![min_{[2;4]}f(x)=-min_{[-4;-2]}f(x)=1\\max_{[2;4]}f(x)=-max_{[-4;-2]}f(x)=-3](/tpl/images/1407/6823/5cc0f.png)
4.
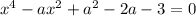
Это биквадратное уравнение. Делаем подстановку
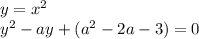
Уравнение будет иметь один корень, когда дискриминант равен 0
Но, поскольку х=±√у, то при любом положительном у мы получим два различных значения х. Одно значение х мы получим лишь в случае у=0. Тогда х=√0=0. Следовательно
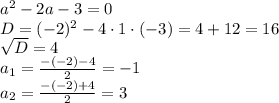
Делаем проверку:
1) а=-1

Имеется одно решение (т.к выражение в скобках никогда не будет равно 0)
2) а=3
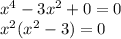
Здесь появляется второй корень. Значит, это значение не подходит.
Окончательно получаем решение: а=-1
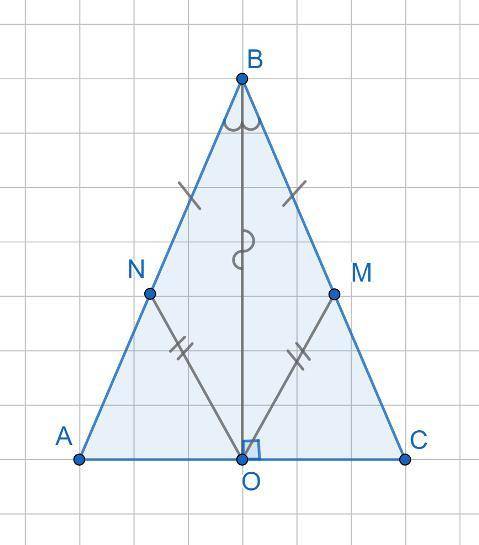
Дано: ΔABC равнобедренный; AB = BC; BO высота; BN = BM.
Доказать: NO = MO.
Доказательство:
ΔBNO = ΔBMO по 1 признаку равенства треугольников (по двум сторонам и углу между ними).
BN = BM по условию;
BO общая сторона;
∠NBO = MBO, т.к. высота в равнобедренном треугольнике является медианой и биссектрисой. Высота BO является биссектрисой ∠NBM, т.е. делит его на на два равных угла.
Из равенства треугольников следует равенство соответствующих сторон. NO = MO, что и требовалось доказать.
Рисунок в приложении.
sinα = -√91/10, α∈(3п/2;2П) - это означает, что угол α находится в 4-й четверти,
cosα - положительный.
Найдем cosα по формуле: cos²α= 1 - sin²α; cos²α= 1-(-√91/10)²=1-91/100=9/100;
cosα = √(9/100)=3/10;
ответ: cosα = 3/10;