Найдём производную функции
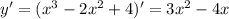
Теперь найдём критические точки(y'=0):
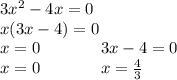
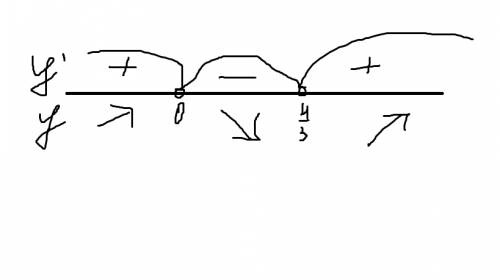
Начертим прямую, нанесём точки на интервал. Там где производная положительная функци возрастает, отрицательная убывает. Там где функция сначало возрастала(убывала), а после в какой-то точке начало убывать(возрастать), то это точка экстрэмума.
Вложение.
Промежутки возрастания, убывания(промежутки монотонности):
(-бесконечности;0] - возрастает
(0;4/3] - убывает
(4/3;+бесконечности) - возрастает.
Экстэмумы функции: 0 - точка максимума.
4/3 - точка минимума.
Рисунок вложение.
Чтобы найти наибольшее и наименьшее значение на отрезке нужно найти значения на функции на концах отрезков, и на точках которые входят в этот промежуток. У нас это точки: -1;4;0;4/3
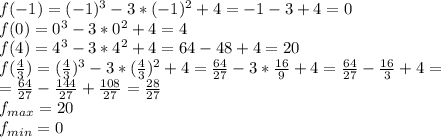
уравнение касательной:
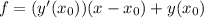
Найдём y(x0):
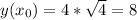
Найдём производную.
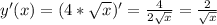
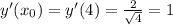
Подставим в уравнение касательной.
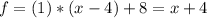
9\x-36*3\x^3+3=0 домножим на x^3
3x^3-9x^2-108=0
а дальше по инструкции
Инструкция 1Кубическое уравнение в общем виде выглядит так: ax³ + bx² + cx + d = 0, a не равно 0; a, b, c, d - вещественные числа. Универсальным методом решения уравнения третьей степени является метод Кардано.
2Для начала приводим уравнение к виду y³ + py + q = 0. Для этого производим замену переменной x на y - b/3a. Подстановку замены смотрите на рисунке. Для раскрытия скобок используются две формулы сокращенного умножения: (a-b)³ = a³ - 3a²b + 3ab² - b³ и (a-b)² = a² - 2ab + b². Затем приводим подобные слагаемые и группируем по степеням переменной y.
3Теперь, чтобы получить при y³ единичный коэффициент, делим все уравнение на a. Тогда получим следующие формулы для коэффициентов p и q в уравнении y³ + py + q = 0.
4Затем вычисляем специальные величины: Q, α, β, которые позволят вычислить корни уравнения с y.
5Тогда три корня уравнения y³ + py + q = 0 вычисляются по формулам на рисунке.
6Если Q > 0, то уравнение y³ + py + q = 0 имеет только один вещественный корень y1 = α + β (и два комплексных, вычислите их по соответствующим формулам, если необходимо).
Если Q = 0, то все корни вещественны и по крайней мере два из них совпадают, при этом α = β и корни равны: y1 = 2α, y2 = y3 = -α.
Если Q < 0, то корни вещественны, но необходимо умение извлекать корень из отрицательного числа. После нахождения y1, y2 и y3 подставьте их в замену x = y - b/3a и найдите корни первоначального уравнения.
бери......................