Функция убывает при x ∈ [- 2; 0] ; [2; + ∞).
Функция возрастает при x ∈ (- ∞; - 2] ; [0; 2].
Объяснение:
y = - x⁴ + 8x² - 16
y' = - 4x³ + 16x
y' = 0
- 4x³ + 16x = 0
4x(x² - 4) = 0
x = 0, x² - 4 = 0
(x - 2)(x + 2) = 0
x = 2 x = - 2
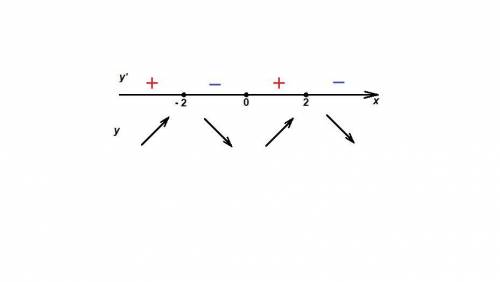
Отметим точки на координатной прямой и определим знаки производной на получившихся интервалах (знаки чередуются, справа минус), см. рисунок.
Если на промежутке производная положительна, то функция возрастает, если отрицательна - убывает.
Функция убывает при x ∈ [- 2; 0] ; [2; + ∞).
Функция возрастает при x ∈ (- ∞; - 2] ; [0; 2].
(-сos2a+sin2a)/(cos2a)=tg2a-1
(cos^2a+cos^2asina)/(1+sina)=cos^2a=3/4
3sin^2a+(1-sin^2a)^2=3sin^2a+sin^4a-2sin^2a+1=1+sin^2a+sin^4a
=1
(3sin^2a-2)/cosa(3sina+cosa)
sin^2a+sin^2b-sin^asin^2b+1-sin^2a-sin^2b+sin^2asin^2b=1