Question

X²+px+2=0, sin²pi*p+ sin²pi*x+2^|y|=|sinpi*x/2|. при каких p система имеет решения?​

Answer 1

±3

Объяснение:

Рассмотрим второе уравнение.

$\sin^2 {\pi p}\geq 0,\ \sin^2 {\pi x}\geq 0, 2^{|y|}\geq 2^0 = 1\Rightarrow\\\Rightarrow \sin^2 {\pi p}+\sin^2 {\pi x}+2^{|y|} \geq 0+0+1=1$

$|\sin{\dfrac{\pi x}{2}}|\leq 1$

Левая часть не меньше 1, правая — не больше 1, значит, равенство возможно тогда и только тогда, когда когда обе части равны 1. При этом левая часть равна 1 только тогда, когда первые два слагаемых — 0, а второе — 1.

$\begin{cases}\sin^2{\pi p}=0, \\ \sin^2{\pi x}=0, \\ 2^{|y|} = 1, \\ |\sin{\dfrac{\pi x}{2}}|=1 \end{cases} \begin{cases}\pi p=\pi k, k\in\mathbb{Z}, \\ \pi x=\pi m, m\in\mathbb{Z}, \\ y=0, \\ \dfrac{\pi x}{2}=\dfrac{\pi}{2}+\pi n, n\in\mathbb{Z} \end{cases} \begin{cases}p\in\mathbb{Z}, \\ x\in\mathbb{Z}, \\ y=0, \\ x= 1+2 n, n\in\mathbb{Z} \end{cases}$

Из этого следует, что решениями системы могут быть пары вида (x, 0), где x — нечётное целое число, а параметр p — целое число.

Рассмотрим первое уравнение:

$D=p^2-8$

Необходимое условие для целочисленности x — дискриминант должен быть квадратом целого числа (достаточно, чтобы это число было неотрицательным), иначе корень будет иррациональным.

$p^2-8=n^2, n\in\mathbb{Z}, n\geq 0\\p^2-n^2=8\\(p-n)(p+n)=8$

Так как n ≥ 0,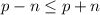 $p-n\leq p+n$.

Представим 8 в виде произведения двух множителей: 8 = 1 * 8 = 2 * 4 = (-8) * (-1) = (-4) * (-2). Числа p - n и p + n имеют одинаковую чётность, поэтому варианты p - n = 1, p + n = 8; p - n = -8, p + n = -1 не подходят. Остаётся два варианта:

$\left \{ {{p-n=2} \atop {p+n=4}} \right. \Rightarrow p = 3, n = 1\\\left \{ {{p-n=-4} \atop {p+n=-2}} \right. \Rightarrow p = -3, n = 1$

Проверим данные p:

$x^2+3x+2=0 \Leftrightarrow (x+2)(x+1)=0 \Leftrightarrow x=-2; -1$

Есть нечётное решение x = -1.

$x^2-3x+2=0 \Leftrightarrow (x-2)(x-1)=0 \Leftrightarrow x=1; 2$

Есть нечётное решение x = 1.

Значит, подходят p = ±3.