Решить ,буду рад решению любого 5. побудуйте графік функції y=3+2x-x2. використовуючи графік, знайдіть: 1) множину значень функції; 2) проміжок, на якому вона спадає. 6. перший член арифметичної прогресії дорівнює 4, а її різниця 3.скільки треба взяти перших членів прогресії, щоб їх сума була рівна 246? 7. доведіть, що х2 + 5у2 + 4ху – 4у + 4 0 при усіх дійсних значеннях х і у. 8. висота, проведена до гіпотенузи прямокутного трикутника, ділить її на два відрізки 18 і32 см. знайдіть площу трикутника.

👇

Ответ:

Polymesiz

31.03.2020

8) Высота, проведённая из вершины прямого угла к гипотенузе является средним пропорциональным между отрезками, на которые делится гипотенуза основанием высоты, то есть h²=a*b, где а=18, b=32

h²=576, h=24

Гипотенуза с=a+b=18+32=50

Площадь S=1/2*h*c=1/2*24*50=600

6) a₁=4, d=3 S(n)=246

S(n)=[ (2a₁+d(n-1)) /2 ]*n

2*4+3n-3

S(n)= * n =246

3n²+5n-492=0 , D=25+4*3*492=5929 , √D=77 ,

n₁=(-5-77)/6=-82/6=-41/3

n₂=(-5+77)/6=72/6=12

Надо взять первых 12 членов прогрессии, чтобы получить S=246

5) Чтобы построить график, надо определить несколько характерных точек для кривой и провести через них кривую.

Заданная ф-ция - парабола.Так как перед х² коэффициент равен (-1), то ветви параболы направлены вниз. Поэтому наибольшее значение ф-ция принимает в вершине.

Точки пересечения с осью ОХ: 3+2х-х²=0 ⇒ х²-2х-3=0

По теореме Виета х₁=-1 , х₂=3 ⇒ точки А(-1,0) и В(3,0) пересечения с ОХ.

Вершина параболы: х(верш)=-b/2a=-2/-2=1 , y(верш)=3+2*1-1²=3+2-1=4

Точка С(1,4) - вершина параболы. ⇒ Наибольшее значение ф-ция у=3+2х-х² - это число 4,значит множество значений ф-ции Е(у)=(-∞,4].

Промежуток убывания - (1,+∞).

4,8(26 оценок)

Открыть все ответы

Ответ:

almira132

31.03.2020

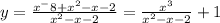
$y=\frac{x^-8+x^2-x-2}{x^2-x-2} =\frac{x^3}{x^2-x-2} +1$

1. Область определения:

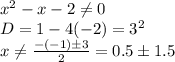
$x^2-x-2\neq 0\\D=1-4(-2)=3^2\\x\neq \frac{-(-1)б3}{2} =0.5б1.5$

x∈(-∞;-1)∪(-1;2)∪(2;+∞)

2. Найдём точки пересечения с осями:

$y=\frac{x^3+x^2-x-2}{x^2-x-2}=0\\y(0)=-2/-2=1\\x^3+x^2-x-2=0\\ax^3+bx^2+cx+d=0\\a=1;b=1;c=-1;d=-2\\p=\frac{3ac-b^2}{3a^2} =\frac{-3-1}{3} =-4/3\\q=\frac{2b^3-9abc+27a^2d}{27a^3} =\frac{2+9-27*2}{27} =-43/27\\x=\sqrt[3]{\frac{-q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}} +\sqrt[3]{\frac{-q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}} -\frac{b}{3a} =\\\sqrt[3]{\frac{43}{2*27}+\sqrt{\frac{43^2}{27^2*4}+\frac{-64}{27*27}}} +\sqrt[3]{\frac{43}{2*27}-\sqrt{\frac{43^2}{27^2*4}+\frac{-64}{27*27}}} -\frac{1}{3}=$

$=\sqrt[3]{\frac{43}{2*27}+\frac{3\sqrt{3*59}}{27*2} }+\sqrt[3]{\frac{43}{2*27}-\frac{3\sqrt{3*59}}{27*2}}-\frac{1}{3}=\\\frac{\sqrt[3]{2(43+3*\sqrt{3*59})}+\sqrt[3]{2(43-3*\sqrt{3*59})}-2}{6}=1.206...$

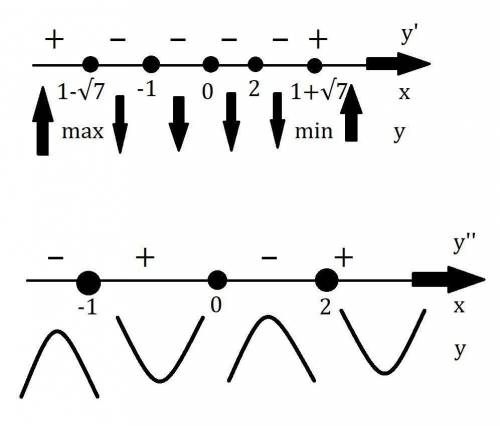
3. Исследование с первой производной:

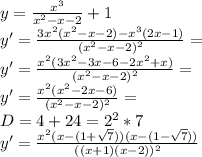
$y=\frac{x^3}{x^2-x-2} +1\\y'=\frac{3x^2(x^2-x-2)-x^3(2x-1)}{(x^2-x-2)^2}=\\ y'=\frac{x^2(3x^2-3x-6-2x^2+x)}{(x^2-x-2)^2}=\\ y'=\frac{x^2(x^2-2x-6)}{(x^2-x-2)^2}=\\D=4+24=2^2*7\\ y'=\frac{x^2(x-(1+\sqrt{7} ))(x-(1-\sqrt{7}))}{((x+1)(x-2))^2}$

Смотри внизу.

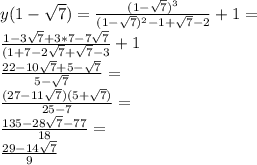
$y(1-\sqrt{7} )=\frac{(1-\sqrt{7} )^3}{(1-\sqrt{7})^2-1+\sqrt{7}-2}+1=\\\frac{1-3\sqrt{7}+3*7-7\sqrt{7} }{(1+7-2\sqrt{7}+\sqrt{7}-3}+1\\\frac{22-10\sqrt{7}+5-\sqrt{7} }{5-\sqrt{7}}=\\\frac{(27-11\sqrt{7})(5+\sqrt{7} )}{25-7} =\\\frac{135-28\sqrt{7}-77}{18} =\\\frac{29-14\sqrt{7} }{9}$

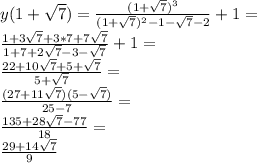
$y(1+\sqrt{7} )=\frac{(1+\sqrt{7})^3}{(1+\sqrt{7})^2-1-\sqrt{7}-2} +1=\\\frac{1+3\sqrt{7}+3*7+7\sqrt{7} }{1+7+2\sqrt{7}-3-\sqrt{7} }+1=\\\frac{22+10\sqrt{7}+5+\sqrt{7} }{5+\sqrt{7}}=\\\frac{(27+11\sqrt{7})(5-\sqrt{7})}{25-7}=\\\frac{135+28\sqrt{7}-77}{18}=\\\frac{29+14\sqrt{7}}{9}$

4. Исследование с второй производной:

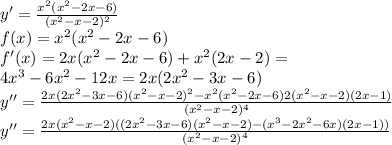
$y'=\frac{x^2(x^2-2x-6)}{(x^2-x-2)^2}\\f(x)=x^2(x^2-2x-6)\\f'(x)=2x(x^2-2x-6)+x^2(2x-2)=\\4x^3-6x^2-12x=2x(2x^2-3x-6)\\y''=\frac{2x(2x^2-3x-6)(x^2-x-2)^2-x^2(x^2-2x-6)2(x^2-x-2)(2x-1)}{(x^2-x-2)^4}\\ y''=\frac{2x(x^2-x-2)((2x^2-3x-6)(x^2-x-2)-(x^3-2x^2-6x)(2x-1))}{(x^2-x-2)^4}$

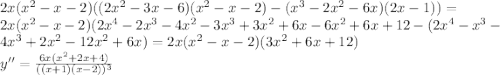
$2x(x^2-x-2)((2x^2-3x-6)(x^2-x-2)-(x^3-2x^2-6x)(2x-1))=\\2x(x^2-x-2)(2x^4-2x^3-4x^2-3x^3+3x^2+6x-6x^2+6x+12-(2x^4-x^3-4x^3+2x^2-12x^2+6x)=2x(x^2-x-2)(3x^2+6x+12)\\y''=\frac{6x(x^2+2x+4)}{((x+1)(x-2))^3}$

Выражение в скобках в числителе всегда положительное и не равняется нулю, смотри вниз.

y(0)=1

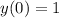
5. Уравнение асимптот:

Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:

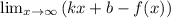
$\lim_{x\to\infty}{(kx+b-f(x))}$

Находим коэффициент k:

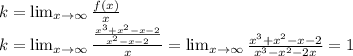
$k=\lim_{x\to\infty}{\frac{f(x)}{x}}\\k=\lim_{x\to\infty}{\frac{\frac{x^{3}+x^{2}-x-2}{x^{2}-x-2}}{x}}=\lim_{x\to\infty}{\frac{x^{3}+x^{2}-x-2}{x^{3}-x^{2}-2x}}=1$

Находим коэффициент b:

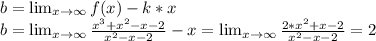
$b=\lim_{x\to\infty}{f(x)-k*x}\\b=\lim_{x\to\infty}{\frac{x^{3}+x^{2}-x-2}{x^{2}-x-2}-x}=\lim_{x\to\infty }{\frac{2*x^{2}+x-2}{x^{2}-x-2}}=2$

Получаем уравнение наклонной асимптоты: у=x+2

Найдем вертикальные асимптоты. Для этого определим точки разрыва: x_1=-1;x_2=2

Находим переделы в точке x=-1

$\lim_{x\to-1-0}{\frac{x^{3}+x^{2}-x-2}{x^{2}-x-2}}=-\infty\\\lim_{x\to-1+0}{\frac{x^{3}+x^{2}-x-2}{x^{2}-x-2}} =\infty$

Это точка разрыва II рода и является вертикальной асимптотой.

Находим переделы в точке x=2

$\lim_{x\to2-0}{\frac{x^{3}+x^{2}-x-2}{x^{2}-x-2}}=-\infty\\\lim_{x\to2+0}{\frac{x^{3}+x^{2}-x-2}{x^{2}-x-2}}=\infty$

Это точка разрыва II рода и является вертикальной асимптотой.

Опираясь на эти записи можно построить график данной функции.

4,5(39 оценок)

Ответ:

zorynastya

31.03.2020

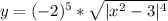
$y=(-2)^5*\sqrt{|x^2-3|^4}$

Т.к. модуль возводиться в чётную степень, от него можно избиваться.

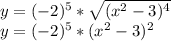
$y=(-2)^5*\sqrt{(x^2-3)^4}\\y=(-2)^5*(x^2-3)^2$

1. Область определения все числа.

2. От х берётся чётная степень, поэтому функция чётная (со словами просто совпадение), то есть y(x)=y(-x), таким образом можно построить график функции справа и отразить его на лево.

3. Найдём точки пересечения с осями:

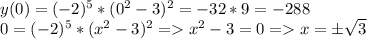
$y(0)=(-2)^5*(0^2-3)^2=-32*9=-288\\0=(-2)^5*(x^2-3)^2=x^2-3=0=x=б\sqrt{3}$

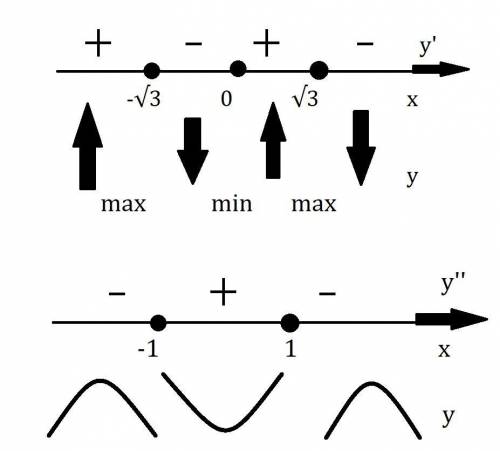
4. Исследование с первой производной (экстремумы и возрастания и убывание функции).

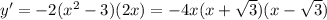
$y'=-2(x^2-3)(2x)=-4x(x+\sqrt{3} )(x-\sqrt{3} )$

Cм. внизу

5. Исследование с второй производной (точки перегиба, выпуклости и вогнутости).

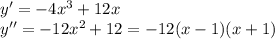
$y'=-4x^3+12x\\y''=-12x^2+12=-12(x-1)(x+1)$

См. внизу

6. Исследование на асимптоты:

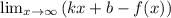
$\lim_{x \to \infty }{(kx+b-f(x))}$

Формула чтобы найти уравнение асимптоты. Найдём k.

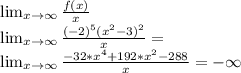
$\lim_{x\to\infty }{\frac{f(x)}{x}}\\\lim_{x \to\infty }{\frac{(-2)^{5}(x^{2}-3)^{2}}{x}}=\\\lim_{x\to\infty }{\frac{-32*x^{4}+192*x^{2}-288}{x}} = -\infty$