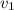, а автобуса 
, 
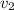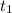время движения автобуса во второй пункт, скорость в нашей системе 
, 
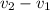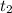час простоя автобуса(его скорость относительно велосипедиста 
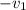, ну и 
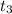момент с начала возвращения автобуса до встречи с велосипедистом,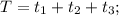 
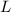расстояние между пунктами, а 
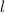растояние, которое проехал велосипедист
,
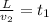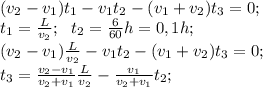
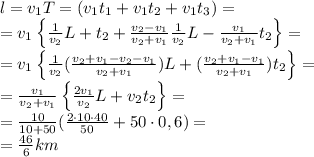
Найти область определение функций
Рассмотрим D (у)
y=x^2 ⇒ D (у) - всё множество действительных чисел, х ∈ (-∞; +∞)
y=2x^2 ⇒ D (у) - всё множество действительных чисел, х ∈ (-∞; +∞)
y=3x^2 ⇒ D (у) - всё множество действительных чисел, х ∈ (-∞; +∞)
y=1/2x^2 ⇒ D (у) - всё множество действительных чисел, кроме х = 0, т.к. на 0 делить НЕЛЬЗЯ х ∈ (-∞; 0) U (0; +∞)
y=1/3x^2 ⇒ D (у) - всё множество действительных чисел, кроме х = 0 т.к. на 0 делить НЕЛЬЗЯ х ∈ (-∞; 0) U (0; +∞)