1.
а)x^3-2x = х(х²-2)
б)5a^2-10ab+5b^2 = 5(a^2-2ab+b^2) = 5(a-b)²
в)cm-cn+3m-3n = (cm-cn)+(3m-3n) = с(m-n)+3(m-n) = (с+3)(m-n)
2.
2(p+q)²-p(4q-p)+q² = 3p²+3q² при любых p и q
2(p+q)²-p(4q-p)+q² = 2(p²+2pq+q²) -4pq+p²+q² = 2p²+4pq+2q² -4pq+p²+q² = 3p²+3q²
таким образом, мы привели левую часть к правой, тем самым доказав, что значения выражений будут равны при любых p и q
3.
(x-3)(x+3) = x(x-2)
х²-9=х²-2х
2х=9
х=4,5
ответ: при х=4,5
4.
а)(a-3b)(a+3b)+(2b+a)(a-2b) = (a²-9b²) + (a²-4b²) = 2a²-13b²
б)(p+q)(q-p)(q²+p²) = (q²-p²)(q²+p²) = q⁴-p⁴
5.
x³-27-3x(x-3)=0
(x³-3³)-3x(x-3)=0
воспользуемся формулой разности кубов:
(х-3)(х²+3х+9)-3x(x-3)=0
(х-3)(х²+3х+9-3х)=0
х-3=0 или (х²+3х+9-3х)=0
х=3 х²+9=0
х²=-9 - решений нет
ответ: х=3
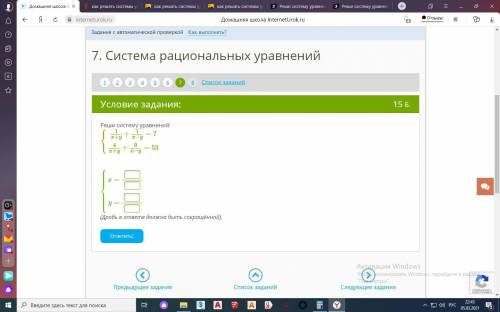
1/(x+y) + 1/(x-y) = 7
4/(x+y) + 9/(x-y) = 53
Пусть 1/(x+y) = t, а 1/(x-y0 = u, тогда
t + u = 7
4t + 9u = 53
Умножим первое уравнение на -4
-4t - 4u = -28
4t + 9u = 53
Сложим оба уравнения
4t - 4t + 9u - 4u = 53 -28
5u = 25
Значит, u = 5
Так как t + 5 = 7, то t = 2
1/(x+y) = 2
1/(x-y) = 5
x + y = 1/2
x - y = 1/5
x = (1/2-y)
(1/2-y) - y = 1/5
x = (1/2-y)
1/2 - 2y = 1/5
x = (1/2-y)
2y = 1/2-1/5
x = (1/2-y)
2y = 3/10
x = (1/2-y)
y = 3/20
x = 1/2-3/20
y = 3/20
x = 7/20
y = 3/20
ответ: 7/20 и 3/20