можно лучший ответ плысссссссс ✌
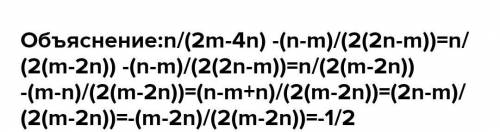
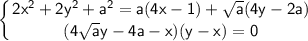
ОДЗ: a ≥ 0
Геометрия уравнений:
· 1-ое уравнение системы можно представить в виде
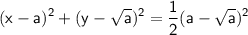
- это уравнение окружности с центром, движущимся по кривой y=√x и радиусом (a-√a)/√2.
· 2-ое уравнение - совокупность двух прямых
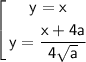
1) Исследуем взаимное расположение первой прямой и окружности. Подставим y = x в первое уравнение системы. Получим квадратное уравнение:
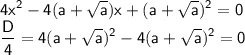
⇒ прямая y = x является касательной к окружности при любых a ≥ 0, что дает нам одно решение системы:
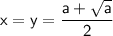
(!) Заметим, что при a = 0 и a = 1 окружность вырождается в точку (0, 0) и (1, 1) соответственно ⇒ система имеет только одно решение при этих значениях a.
2) Исследуем взаимное расположение второй прямой и окружности. Подставим y = (x+4a)/(4√a) в первое уравнение системы. Получим квадратное уравнение:
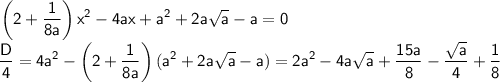
Оценим дискриминант при значениях a = 2, a = 3, a ≥ 4:
· a = 2
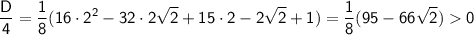
т.к. 95/66 = (99 - 4)/66 = 1.5 - (2/33) > 1.5 - (7/100) = 1.43 > √2 ≈ 1.41
· a = 3
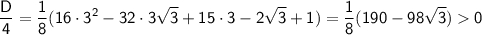
т.к. 190/98 = (196-6)/98 = 2 - (6/98) > 2 - (7/100) = 1.93 > √3 ≈ 1.73
· a ≥ 4
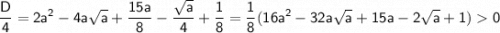
- очевидно, т. к.
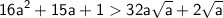
ведь
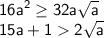
Таким образом, при целочисленном a ≥ 2 прямая пересекает окружность в двух различных точках и, соответственно, дает 2 решения системы. Убедимся что они не совпадают с полученным ранее решением при целочисленных a. Для этого подставим x = y = = (a + √a)/2 в уравнение y = (x + 4a)/(4√a), откуда найдем a = (33+5√41)/32 - не явл. целочисленным.
При a = 0 и a = 1 система имеет одно решение. При a ≥ 2, a ∈ Z система имеет 3 решения.
ответ: при любых целочисленных a ≥ 0.см ниже
Объяснение:
1) рассмотрим ΔEOD и ΔFOС, у них OF=OE и OD=OC по условию, а ∠EOD = ∠FOС как вертикальные углы при EF∩DC. Следовательно ΔEOD = ΔFOС по двум сторонам и углу между ними
2) рассмотрим ΔEOА и ΔFOB, у них OF=OE и ∠OFB=∠OEA по условию, а ∠EOA = ∠FOB как вертикальные углы при EF∩AB. Следовательно, ΔEOA = ΔFOB по двум углам и прилежащей к ним стороне
3) рассмотрим ΔAOD и ΔBOС, у них OD=OC по условию, а ∠AOD = ∠BOС как вертикальные углы при AB∩DC, AO=OB из 2). Следовательно, ΔАOD = ΔВOС по двум сторонам и углу между ними
ответ:m+n/n-m.
Объяснение:n/(2m-4n) -(n-m)/(2(2n-m))=n/(2(m-2n)) -(n-m)/(2(2n-m))=n/(2(m-2n)) -(m-n)/(2(m-2n))=(n-m+n)/(2(m-2n))=(2n-m)/(2(m-2n))=-(m-2n)/(2(m-2n))=-1/2