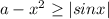
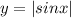расположен выше оси ОХ. 
.
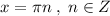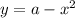- это параболы , ветви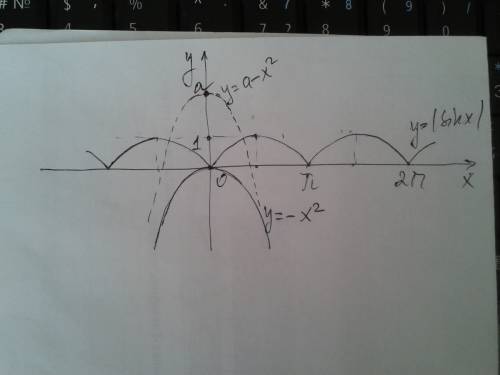
Для нахождения решения корней x2 - 6x = 16 полного квадратного уравнения мы начнем с того, что перенесем 16 в левую часть уравнения:
x2 - 6x - 16 = 0.
Для решения уравнения будем использовать формулы для поиска дискриминанта и корней уравнения через дискриминант.
D = b2 - 4ac = (-6)2 - 4 * 1 * (-16) = 36 + 64 = 100;
Корни уравнения мы вычислим по следующим формулам:
x1 = (-b + √D)/2a = (6 + √100)/2 * 1 = (6 + 10)/2 = 16/2 = 8;
x2 = (-b - √D)/2a = (6 - √100)/2 * 1 = (6 - 10)/2 = -4/2 = -2.
ответ: x = 8; x = -2.
Объяснение:
что (x+1)^3+(x+1)m+3 кратно 3
x^3+mx+3 кратно 3 по предположению
если 1+m+3x+3 кратно 3 по индукции предположение верно
но 3х+3 кратно 3. значит нада что бы 1+m было кратон 3
m=3k-1 k-целое
б) (x+1)^2-4+m(x+1)=(x^2-4+mx)+2x+1+m
1+m-четное m=2k-1