1) 2^(x+1) < 2^5 => x+1 < 5 => x<4
2) 0.2 ^ (3x -4) > 0.2^0 => 3x -4 >0 => 3x >4 => x > 4/3
3) 0.3^(2x -1) > 0.3 ^1 => 2x-1>1 => 2x>2 => x>1
4)0.5^(2x - 1) < 0.5^0 => 2x -1 <0 => 2x <1 => x < 0.5
5) 3 ^(6 - x) > 3^0 => 6 - x >0 => x<6
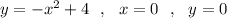
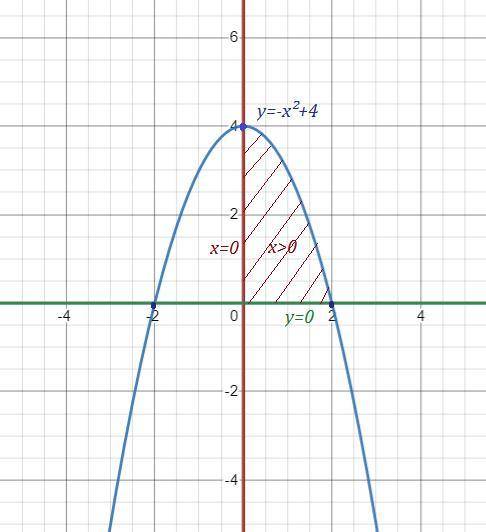
Если задано х=0, то непонятно, площадь какой области находить, слева или справа от прямой х=0. Если задано х>0 , то тогда это правая область, если х<0 , то тогда это левая область . Если вообще не было бы написано уравнение х=0, то эта область находится под параболой до оси ОХ (у=0) .
Найдём площадь правой области при условии х>0 . Если нужна площадь левой области, то она такая же, как и площадь правой области в силу симметрии криволинейной трапеции . Если нужна площадь всей области между параболой и осью ОХ , то она равна удвоенной площади правой области .
Точки пересечения:
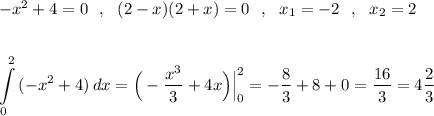
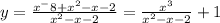
1. Область определения:
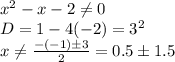
x∈(-∞;-1)∪(-1;2)∪(2;+∞)
2. Найдём точки пересечения с осями:
![y=\frac{x^3+x^2-x-2}{x^2-x-2}=0\\y(0)=-2/-2=1\\x^3+x^2-x-2=0\\ax^3+bx^2+cx+d=0\\a=1;b=1;c=-1;d=-2\\p=\frac{3ac-b^2}{3a^2} =\frac{-3-1}{3} =-4/3\\q=\frac{2b^3-9abc+27a^2d}{27a^3} =\frac{2+9-27*2}{27} =-43/27\\x=\sqrt[3]{\frac{-q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}} +\sqrt[3]{\frac{-q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}} -\frac{b}{3a} =\\\sqrt[3]{\frac{43}{2*27}+\sqrt{\frac{43^2}{27^2*4}+\frac{-64}{27*27}}} +\sqrt[3]{\frac{43}{2*27}-\sqrt{\frac{43^2}{27^2*4}+\frac{-64}{27*27}}} -\frac{1}{3}=](/tpl/images/3195/0622/32bbc.png)
![=\sqrt[3]{\frac{43}{2*27}+\frac{3\sqrt{3*59}}{27*2} }+\sqrt[3]{\frac{43}{2*27}-\frac{3\sqrt{3*59}}{27*2}}-\frac{1}{3}=\\\frac{\sqrt[3]{2(43+3*\sqrt{3*59})}+\sqrt[3]{2(43-3*\sqrt{3*59})}-2}{6}=1.206...](/tpl/images/3195/0622/a8a2e.png)
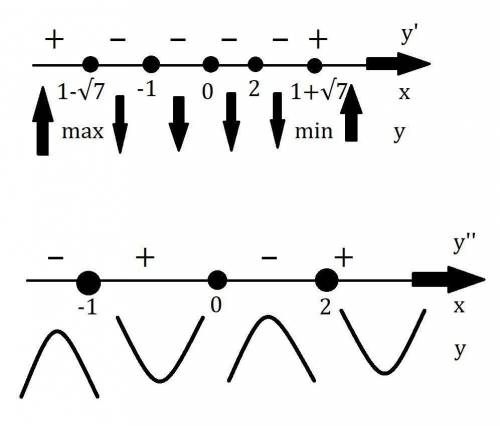
3. Исследование с первой производной:
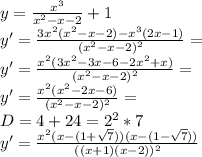
Смотри внизу.
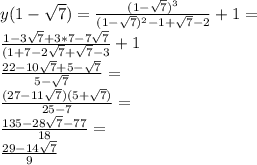
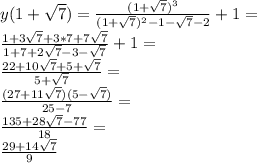
4. Исследование с второй производной:
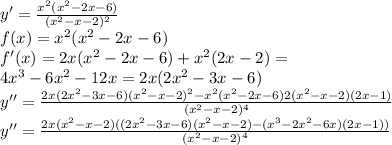
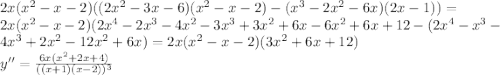
Выражение в скобках в числителе всегда положительное и не равняется нулю, смотри вниз.
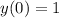
5. Уравнение асимптот:
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:
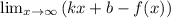
Находим коэффициент k:
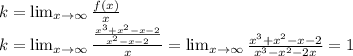
Находим коэффициент b:
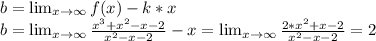
Получаем уравнение наклонной асимптоты: у=x+2
Найдем вертикальные асимптоты. Для этого определим точки разрыва: x_1=-1;x_2=2
Находим переделы в точке x=-1

Это точка разрыва II рода и является вертикальной асимптотой.
Находим переделы в точке x=2

Это точка разрыва II рода и является вертикальной асимптотой.
Опираясь на эти записи можно построить график данной функции.
1) 2^{x+1}<2^5, x+1<5, x<4
2) 0.2^{3x-4}>0.2^0, 3x-4>0, x>4/3
3) 0.3^{2x-1}>0.3^1, 2x-1>1, 2x>2, x>1
4) 0.5^{2x-1}<0.5^0, 2x-1<0, x<1/2
5)3^{6-x}>3^0, 6-x>0, x<6